Find the value of a and b such that the function f(x)={(5a,x≤0),(asinx+cosx,0Solution in Malayalam
Step by step video & image solution for Find the value of a and b such that the function f(x)={(5a,xle0),(asinx+cosx,0<x<pi/2),(b-pi/2,xgepi/2):} is continuous by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
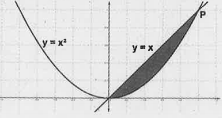
Consider the following figure
find the point of intersection (P) of the parabola and the line.
 02:14View Solution
02:14View SolutionUsing properties of determinants prove
∣∣ ∣ ∣∣xyx+yyx+yxx+yxy∣∣ ∣ ∣∣=−2(x3+y3)11:04View SolutionExamination the function f(t) given by f(x)={cosxπ2−x; for continuity at x=π2
05:24View Solutionthe function f(x)=(6/5)^((tan6x)/(tan5x)) if x is 0 to pi/2 and f(x)=b+2 if x=pi/2 and f(x)=(1+|cosx|)^{(a*|tanx|)/b} if x is pi/2 to pi Determine the values of a&b. if f is continuous at x=pi/2
08:56View SolutionFind the values of A and B if the following function is continuous on [-pi,pi]. f(x) = {((2sinx-sin2x)/x^3,; -pi lt= x lt 0), (Asinx + B cosx,; 0 lt= x lt= pi/2), ((cosecx-1)/(pi//2-x)^2,; pi/2 lt x lt= pi):}
05:08View SolutionIf f(x)=⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩−4sinx+cosxforx≤−π2asinx+bfor−π2<x<π2cosx+2forx≥π2 is continuous, then
05:08View SolutionConsider the function
f(x)=⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩−2sinxifx≤−π2Asinx+Bif−π2<x<π2cosxifx≥π2
Which is continuous everywhere.
The value of A is06:32View SolutionConsider the function
f(x)=⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩−2sinxifx≤−π2Asinx+Bif−π2<x<π2cosxifx≥π2
Which is continuous everywhere.
The value of B is04:41View Solutiona तथा b के मान ज्ञात कीजिये यदि दिया गया फलन दिए गए अंतराल में सतत हो -
f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩x+2asinx,0≤x≤π/32√3cotx+b,π/3≤x≤π/2acos2x−bsinx,π/2≤x≤π02:36View Solutionफलन f(x)=⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩x+a√2sinx,0≤x<π42xcotx+b,π4≤x<π2acos2x−bsinx,π2≤x≤π अंतराल [0,π] में सतत है ।
b का मान ज्ञात कीजिए ।05:57View SolutionThe value of a and b such that the function
f(x)=⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩−2sinx,−π≤x≤−π2asinx+b,−π2<x<π2cosx,π2≤x≤π is continuous in [−π,π] areView SolutionLet f(x)=⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩−2sinx if x≤−π2Asinx+B if −π2<x<π2cosx if x≥π2. Then
View SolutionIf f(x)={(−2sinx,forx≤−π2)(asinx+b,for−π2<x<π2)(cosx,forx≥π2) everywhere then the ordered pair(a,b) is
02:27View SolutionIf f(x)={(−2sinx,forx≤−π2)(asinx+b,for−π2<x<π2)(cosx,forx≥π2) everywhere then the ordered pair(a,b) is
02:06View SolutionDetermine the constants 'a' and 'b' so that the function 'f' defined below is continuous everywhere :
f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩5a, x≤0asinx+cosx, 0<x<π2b−π2, x≥π2.05:25View Solution

