Find the value of p for the following distribution whose mean is 16.6. x:8,12,15,p,20,25,30 and f:12,16,20,24,16,8,4
To find the value of p for the given distribution whose mean is 16.6, we can follow these steps:
Step 1: Set up the data
We have the values of x and their corresponding frequencies f:
- x:8,12,15,p,20,25,30
- f:12,16,20,24,16,8,4
Step 2: Calculate f⋅x for known values
We will calculate the product of each x value and its corresponding frequency f:
- For x=8 and f=12: 8⋅12=96
- For x=12 and f=16: 12⋅16=192
- For x=15 and f=20: 15⋅20=300
- For x=p and f=24: p⋅24=24p
- For x=20 and f=16: 20⋅16=320
- For x=25 and f=8: 25⋅8=200
- For x=30 and f=4: 30⋅4=120
Step 3: Sum of f⋅x
Now we sum these products:
Sum=96+192+300+24p+320+200+120=1228+24p
Step 4: Calculate the total frequency
Next, we calculate the total frequency:
Total frequency=12+16+20+24+16+8+4=100
Step 5: Set up the mean equation
The formula for the mean μ is given by:
μ=∑(f⋅x)∑f
Substituting the known values:
16.6=1228+24p100
Step 6: Solve for p
To eliminate the fraction, multiply both sides by 100:
1660=1228+24p
Now, isolate 24p:
24p=1660−1228
24p=432
Now, divide by 24:
p=43224=18
Final Answer
The value of p is 18.
---
We have the values of x and their corresponding frequencies f:
- x:8,12,15,p,20,25,30
- f:12,16,20,24,16,8,4
We will calculate the product of each x value and its corresponding frequency f:
- For x=8 and f=12: 8⋅12=96
- For x=12 and f=16: 12⋅16=192
- For x=15 and f=20: 15⋅20=300
- For x=p and f=24: p⋅24=24p
- For x=20 and f=16: 20⋅16=320
- For x=25 and f=8: 25⋅8=200
- For x=30 and f=4: 30⋅4=120
Now we sum these products:
Sum=96+192+300+24p+320+200+120=1228+24p
Next, we calculate the total frequency:
Total frequency=12+16+20+24+16+8+4=100
The formula for the mean μ is given by:
μ=∑(f⋅x)∑f
Substituting the known values:
16.6=1228+24p100
To eliminate the fraction, multiply both sides by 100:
1660=1228+24p
Now, isolate 24p:
24p=1660−1228
24p=432
Now, divide by 24:
p=43224=18
The value of p is 18.
Topper's Solved these Questions
Similar Questions
Find the value of for the following distribution whose mean is 16.6.
View SolutionFind the value of p for the following distribution whose mean is 16.6 8 12 15 20 25 30 12 16 20 24 16 8 4
View SolutionFind the value of p for the following distribution whose mean is 12.58. x:5,8,10,12,p,20,25 and f:2,5,8,22,7,4,2
View SolutionFind the missing value of for the following distribution whose mean is 12.58 5 8 10 12 20 25 2 5 8 22 7 4 2
View SolutionFind the value of p, if the mean of following distribution is 20.
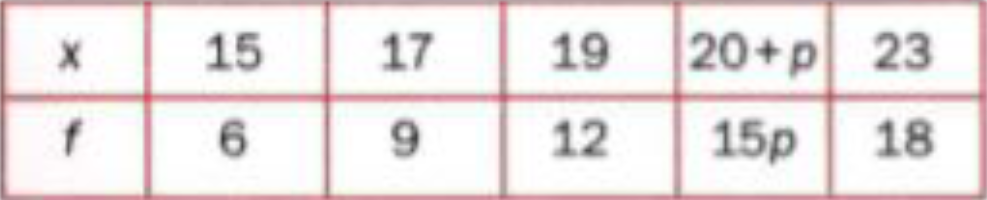 View Solution
View SolutionFind the value of p, if the mean of the following distribution is 20 15 17 19 23 2 3 4 5 6
View SolutionFind the value of p, if the mean of the following distribution is 7.5. x: 3 5 7 9 11 13 f: 6 8 15 p 8 4
View SolutionFind the value of p if the mean of the following distribution is 7.5. 3 5 7 9 11 13 f: 6 8 15 p 8 4
View SolutionFind the value of p , the mean of the following distribution is 7.5 x: 3 5 7 9 11 13 f: 6 8 15 p 8 4
View SolutionFind the value of p , if the mean of the following distribution is 20. x:15,17,19,20+p,23 and f : 2, 3, 4, 5p, 6
View Solution

