Find the value of p, if the mean of the following distribution is 7.5. x: 3 5 7 9 11 13 f: 6 8 15 p 8 4
To find the value of p such that the mean of the given distribution is 7.5, we can follow these steps:
Step 1: Write down the given data
The values of x and their corresponding frequencies f are as follows:
xf36587159p118134
Step 2: Calculate fixi
Now, we will calculate fixi for each value of x:
xffixi363×6=18585×8=407157×15=1059p9×p=9p11811×8=8813413×4=52
Step 3: Sum of f and fixi
Now, we will calculate the summation of f and fixi:
Sum of f=6+8+15+p+8+4=41+p
Sum of fixi=18+40+105+9p+88+52=303+9p
Step 4: Use the mean formula
The formula for the mean ¯x is given by:
¯x=∑fixi∑f
We know that the mean is 7.5, so we can set up the equation:
7.5=303+9p41+p
Step 5: Cross-multiply to solve for p
Cross-multiplying gives us:
7.5(41+p)=303+9p
Expanding this:
307.5+7.5p=303+9p
Step 6: Rearranging the equation
Rearranging the equation to isolate p:
307.5−303=9p−7.5p
This simplifies to:
4.5=1.5p
Step 7: Solve for p
Now, divide both sides by 1.5:
p=4.51.5=3
Conclusion
Thus, the value of p is 3.
---
The values of x and their corresponding frequencies f are as follows:
Now, we will calculate fixi for each value of x:
Now, we will calculate the summation of f and fixi:
The formula for the mean ¯x is given by:
Cross-multiplying gives us:
Rearranging the equation to isolate p:
Now, divide both sides by 1.5:
Thus, the value of p is 3.
Topper's Solved these Questions
Similar Questions
Find the value of if the mean of the following distribution is 7.5
View SolutionFind the value of p, if mean of the following distribution is 7.5.
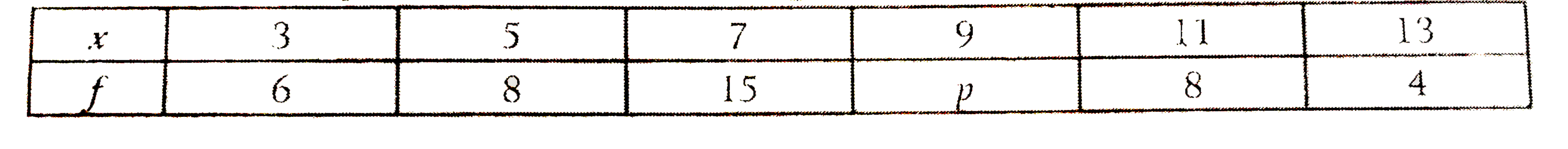 View Solution
View SolutionFind the value of p, if the mean of the following distribution is 20 15 17 19 23 2 3 4 5 6
View SolutionFind the value of p if the mean of the following distribution is 7.5. 3 5 7 9 11 13 f: 6 8 15 p 8 4
View SolutionFind the value of p , the mean of the following distribution is 7.5 x: 3 5 7 9 11 13 f: 6 8 15 p 8 4
View SolutionFind the mean of the following distribution: 4 6 9 10 15 5 10 10 7 8
View SolutionFind the mean of the following distribution: x: 4 6 9 10 15 f: 5 10 10 7 8
View SolutionFind the mean of the following distribution:
x: 4 6 9 10 15
f: 5 10 10 7 8View SolutionFind the mean of the following distribution: x: 4 6 9 10 15 f: 5 10 10 7 8
View SolutionCalculate the mean for the following distribution: 5 6 7 8 9 4 8 14 11 3
View Solution

