find the value of the
±√nπ,n∈{0,1,2,...}
±√nπ,n∈{1,2,...}
π2+2nπ,n∈{...,−2,−1,0,1,2...}
2nπ,n∈{...,−2,−1,0,1,2,...}
The correct Answer is:A
To solve the given problem, we need to find the values of certain trigonometric expressions based on the provided sets. Let's break down the solution step by step.
Step 1: Define the Sets
We will define the sets based on the problem statement:
1. Set A: A={±√nπ∣n∈W} where W is the set of whole numbers (0, 1, 2, 3,...).
2. Set B: B={±√nπ∣n∈N} where N is the set of natural numbers (1, 2, 3,...).
3. Set C: C={π2+2nπ∣n∈Z} where Z is the set of integers (..., -2, -1, 0, 1, 2,...).
4. Set D: D={2nπ∣n∈Z}.
Step 2: Calculate Elements of Set A
For Set A, we will calculate the elements for n=0,1,2,3,4:
- For n=0: ±√0⋅π=0
- For n=1: ±√1⋅π=±√π
- For n=2: ±√2⋅π=±√2π
- For n=3: ±√3⋅π=±√3π
- For n=4: ±√4⋅π=±2√π
Thus, Set A is:
A={0,±√π,±√2π,±√3π,±2√π}
Step 3: Calculate Elements of Set B
For Set B, we will calculate the elements for n=1,2,3,4:
- For n=1: ±√1⋅π=±√π
- For n=2: ±√2⋅π=±√2π
- For n=3: ±√3⋅π=±√3π
- For n=4: ±√4⋅π=±2√π
Thus, Set B is:
B={±√π,±√2π,±√3π,±2√π}
Step 4: Calculate Elements of Set C
For Set C, we will calculate the elements for n=−2,−1,0,1,2:
- For n=0: π2+2⋅0⋅π=π2
- For n=1: π2+2⋅1⋅π=π2+2π=5π2
- For n=−1: π2+2⋅(−1)⋅π=π2−2π=−3π2
- For n=2: π2+2⋅2⋅π=π2+4π=9π2
- For n=−2: π2+2⋅(−2)⋅π=π2−4π=−7π2
Thus, Set C is:
C={π2,5π2,−3π2,9π2,−7π2}
Step 5: Calculate Elements of Set D
For Set D, we will calculate the elements for n=−2,−1,0,1,2:
- For n=0: 2⋅0⋅π=0
- For n=1: 2⋅1⋅π=2π
- For n=−1: 2⋅(−1)⋅π=−2π
- For n=2: 2⋅2⋅π=4π
- For n=−2: 2⋅(−2)⋅π=−4π
Thus, Set D is:
D={0,2π,−2π,4π,−4π}
Final Result
The values of the sets are:
- Set A: A={0,±√π,±√2π,±√3π,±2√π}
- Set B: B={±√π,±√2π,±√3π,±2√π}
- Set C: C={π2,5π2,−3π2,9π2,−7π2}
- Set D: D={0,2π,−2π,4π,−4π}
We will define the sets based on the problem statement:
2. Set B: B={±√nπ∣n∈N} where N is the set of natural numbers (1, 2, 3,...).
3. Set C: C={π2+2nπ∣n∈Z} where Z is the set of integers (..., -2, -1, 0, 1, 2,...).
4. Set D: D={2nπ∣n∈Z}.
For Set A, we will calculate the elements for n=0,1,2,3,4:
- For n=1: ±√1⋅π=±√π
- For n=2: ±√2⋅π=±√2π
- For n=3: ±√3⋅π=±√3π
- For n=4: ±√4⋅π=±2√π
A={0,±√π,±√2π,±√3π,±2√π}
For Set B, we will calculate the elements for n=1,2,3,4:
- For n=2: ±√2⋅π=±√2π
- For n=3: ±√3⋅π=±√3π
- For n=4: ±√4⋅π=±2√π
B={±√π,±√2π,±√3π,±2√π}
For Set C, we will calculate the elements for n=−2,−1,0,1,2:
- For n=1: π2+2⋅1⋅π=π2+2π=5π2
- For n=−1: π2+2⋅(−1)⋅π=π2−2π=−3π2
- For n=2: π2+2⋅2⋅π=π2+4π=9π2
- For n=−2: π2+2⋅(−2)⋅π=π2−4π=−7π2
C={π2,5π2,−3π2,9π2,−7π2}
For Set D, we will calculate the elements for n=−2,−1,0,1,2:
- For n=1: 2⋅1⋅π=2π
- For n=−1: 2⋅(−1)⋅π=−2π
- For n=2: 2⋅2⋅π=4π
- For n=−2: 2⋅(−2)⋅π=−4π
D={0,2π,−2π,4π,−4π}
The values of the sets are:
- Set A: A={0,±√π,±√2π,±√3π,±2√π}
- Set B: B={±√π,±√2π,±√3π,±2√π}
- Set C: C={π2,5π2,−3π2,9π2,−7π2}
- Set D: D={0,2π,−2π,4π,−4π}
Topper's Solved these Questions
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Multiple correct answer type)
2 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Linked comprehension type)
1 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives ((JEE MAIN) Single correct Answer type)
2 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - ARCHIVES INTEGER TYPE
1 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - SINGLE CORRECT ANSWER TYPE
38 Videos
Similar Questions
If A=15∘ , then find the value of sec 2A.
View SolutionF∈dthevalueofy
View SolutionF∈dthevalueofp
View SolutionF∈dthevalueofx
View SolutionF∈dthevalueofx
View SolutionF∈dthevalueofx
View SolutionF∈dthevalueofx
View SolutionIn Figure, find the value of x
View SolutionIn the given ,figure find the value of x .
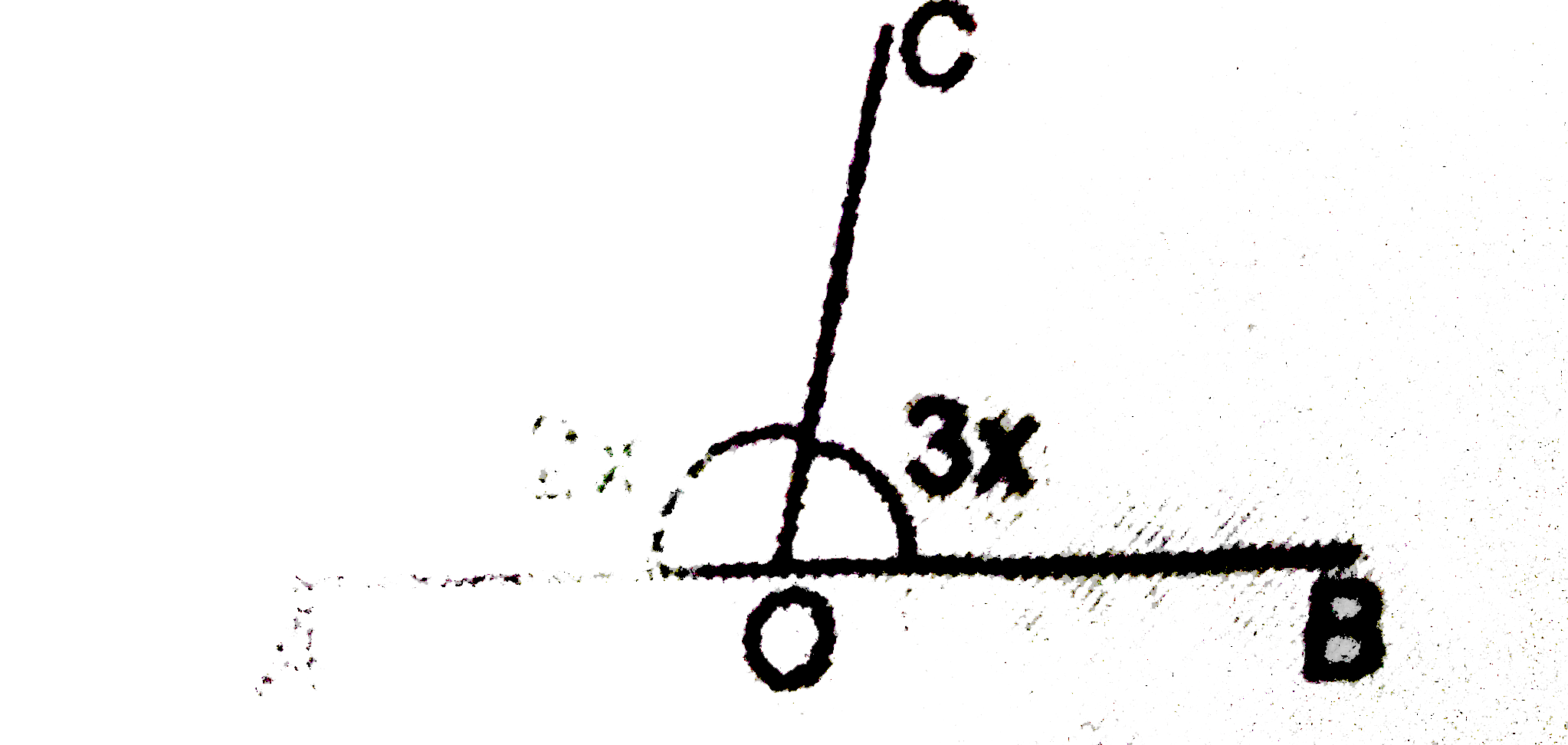
View SolutionIf the mean of is , find the value of
View Solution
