Find the values of b for which the points lies above of the line 3x-4y-a(a-2) = 0 .Solution in Tamil
Given line is 3x-4y-a(a-2)=0
One of the possible lines is as shown in the following figure.
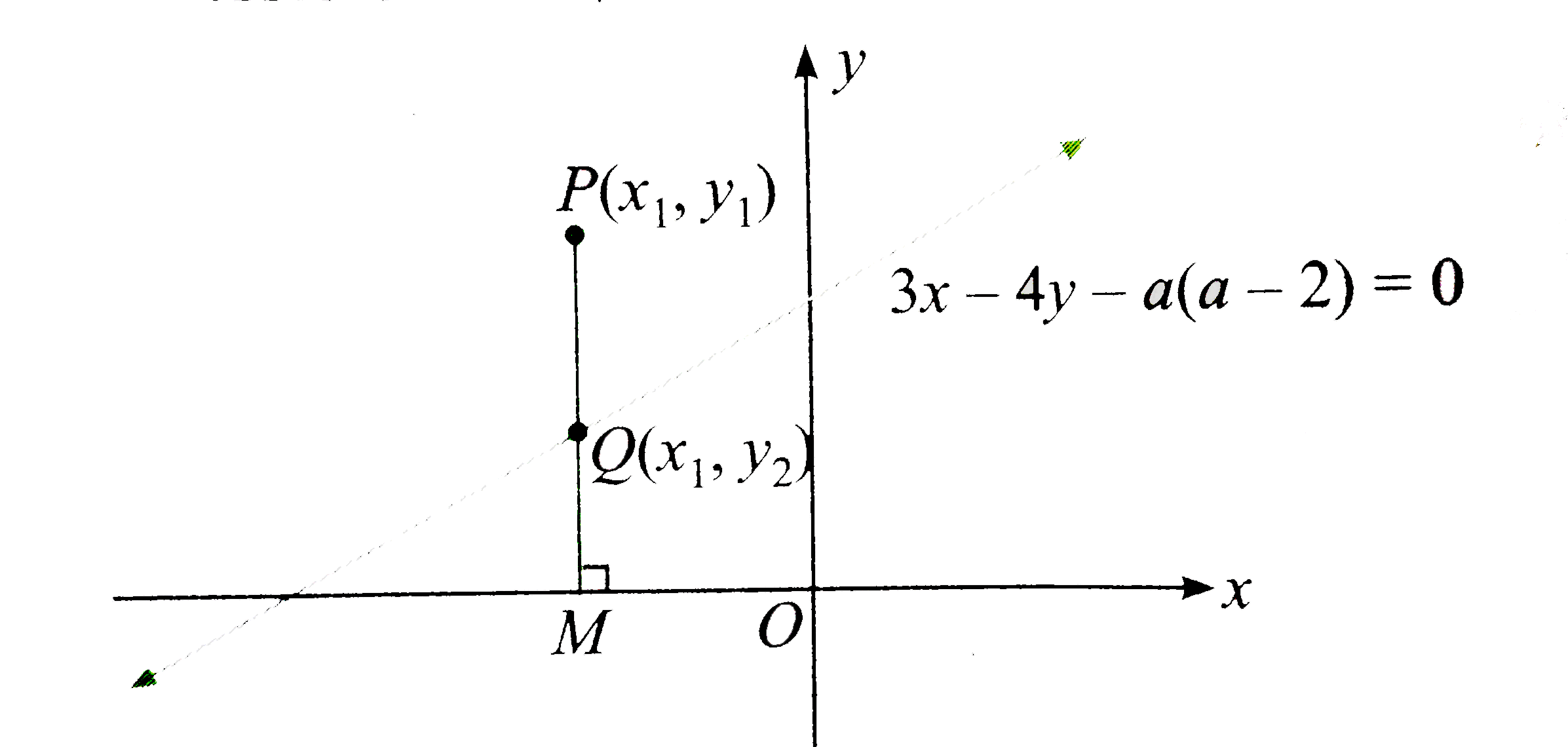
Consider the point lying above this line.
Draw perpendicular from point P to the x-axis meeting the line at
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.1
23 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.2
4 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
Find the equation of the right bisector of the line segment joining the points (3,4) and (−1,2).
View SolutionFind the points on the line x + y = 1 that lie at a distance 3 units from the line 5x+12y = 3.
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
View SolutionOn the straight line y=x+2, a point (a,b) is such that the sum of the square of the distances from the straight lines 3x-4y+8=0 and 3x-y-1=0 is least then find value of 11(a+b)
View SolutionOn the straight line y=x+2 a point (a,b) partney is such that the sum of the source of distances from the tegories lines 3x-4y+8=0 and 3x-y-1=0 is least,then find value of 11(a+b)
View SolutionFind the values of b for which the points (2b+3,b2) lies above of the line 3x-4y-a(a-2) = 0 ∀a∈R.
View Solutiona तथा b के वे मान ज्ञात कीजिए जिसके लिए
[a2+12ba−1b+3]=[2ab2+4b+102].
View SolutionThe maximum negative integral value of b for which the point (2b+3,b2) lies above the line
3x−4y−a(a−2)=0,∀a∈R is
View SolutionFind the equation of a circle which passes through the points (1,-2) and (4,-3) and whose centre lies on the line 3x+4y=0
View SolutionConsider the line 3x – 4y + 2 = 0 and the point (2, -3)
Find the distance of the point from the line.
View SolutionFind equation of the line parallel to the line 3x - 4y + 2 = 0 and passing through the point (-2, 3) .
View SolutionFind equation of the line parallel to the line 3x - 4y + 2 = 0 and passing through the point (-2, 3) .
View SolutionIf the point (3, 4) lies on the locus of the point of intersection of the lines xcosα+ysinα=a and xsinα−ycosα=b (α is a variable), the point (a, b) lies on the line 3x−4y=0 then a2−b22 is equal to
View SolutionIf the point (0, B) lies above or inside a triangle whose sides are y + 3x + 2 = 0,3y-2x-53 = 0 and 4y + x-14 = 0, then
View SolutionFind the values of b for which the points (2b+3,b2) lies above of the line 3x-4y-a(a-2) = 0 ∀a∈R.
View Solution
