Find the values of x∈[0,2π] for which function f(x)=tan−1(tanx)andg(x)=cos−1(cosx) are identicalSolution in Bengali
The correct Answer is:[0,π/2)∪{2π]
Let us draw the graph of both th efunction for x∈[0,2π]
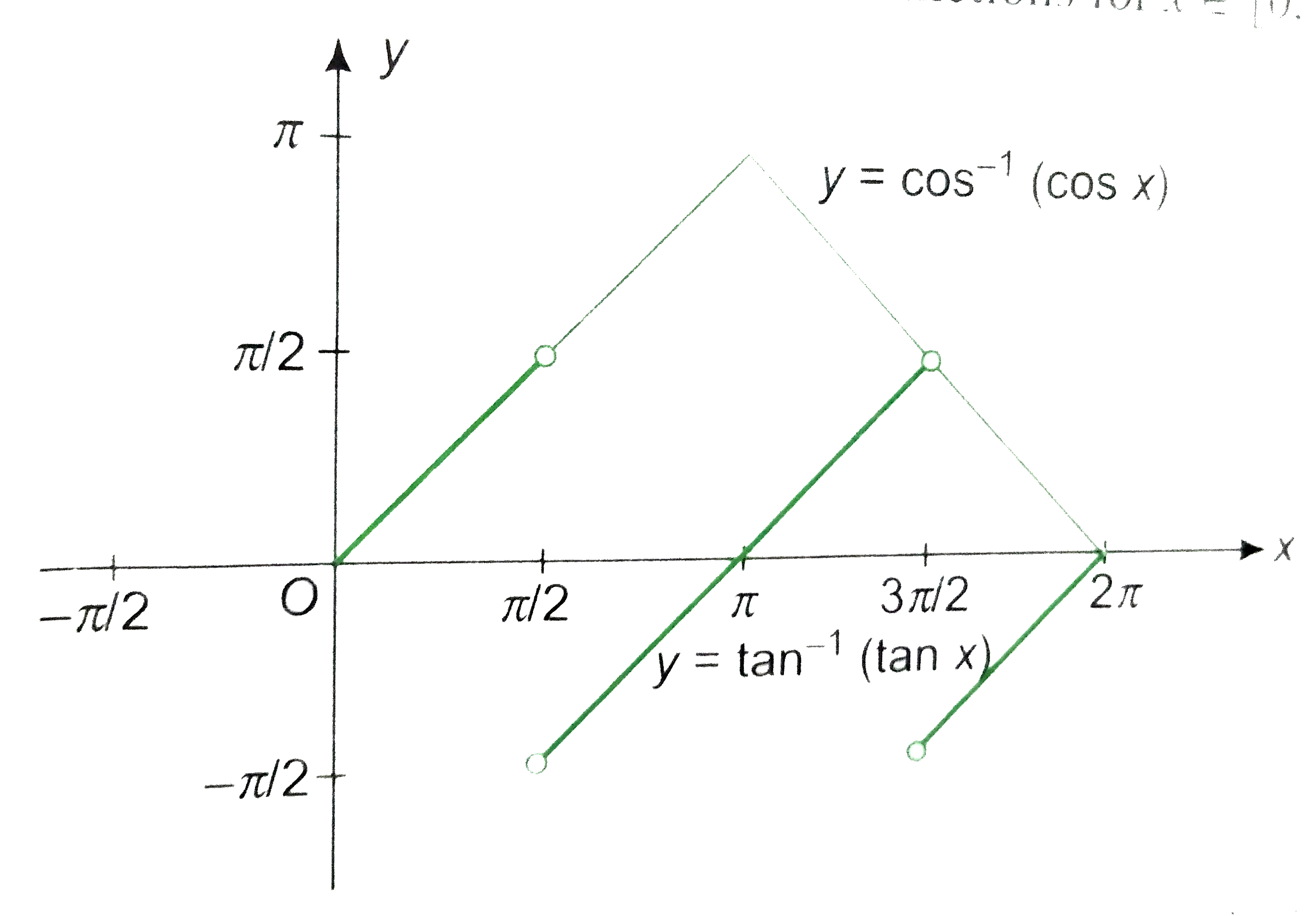
In the above figure, graph of y=f(x)andy=g(x) coincide for x∈[0,π/2)∪{2π}
Topper's Solved these Questions
Similar Questions
The points with position vectors →x+→y,→x−→yand→x+λ→y are collinear for all real values of λ.
View SolutionIf y = y(x) is the solution of the differential equation, xdydx+2y=x2 satisfying y(1) = 1, then y(12) is equal to
View SolutionLet f(x)=sinx+cosx+tanx+sin−1x+cos−1x+tan−1x. Then find the maximum and minimum values of f(x).
View SolutionFind the value of x for which function are identical. f(x)=cosxandg(x)=1√1+tan2x
View SolutionFind the value of x for which function are identical. f(x)=tan−1x+tan−11xandg(x)=sin−1x+cos−1x
View SolutionFind period of the function f(x)=cos(tan x+cot x)cos(tan x-cot x)
View SolutionFind the values of x∈[0,2π] for which function f(x)=tan−1(tanx)andg(x)=cos−1(cosx) are identical
View SolutionFind the values of x for which the following pair of functions are identical.
(i) f(x)=tan−1x+cot−1x and g(x)=sin−1x+cos−1x
(ii) f(x)=cos(cos−1x) and g(x)=cos−1(cosx)
View SolutionFind the value of x for which function are identical. f(x)=cosxandg(x)=1√1+tan2x
View SolutionFind the value of x for which function are identical. f(x)=tan−1x+tan−1(1x)andg(x)=sin−1x+cos−1x
View SolutionFind the values of x∈[0,2π] for which function f(x)=tan−1(tanx)andg(x)=cos−1(cosx) are identical
View SolutionFind the values of x for which the following pair of functions are identical.
(i) f(x)=tan−1x+cot−1x and g(x)=sin−1x+cos−1x
(ii) f(x)=cos(cos−1x) and g(x)=cos−1(cosx)
View Solutionf(x)=tan−1x+tan−1(1x),g(x)=sin−1x+cos−1x are identical function if
View SolutionFind the derivatives of the function
tan−1(cosx1+cosx)
View Solutionf(x)=tan−1x+tan−1(1x);g(x)=sin−1x+cos−1x are identical functions if
View SolutionFind the value of x for which function are identical. f(x)=tan−1x+tan−11xandg(x)=sin−1x+cos−1x
View Solution
