Following frequency distribution given the weights of 38 students of a class: Weight in Kg: 31-35 36-40, 41-45, 46-50, 51-55, 56-60 61-65, 66-70 71-75 No. of students 9 5 14 3 1 2 2 1 1 Find the probability that weight of a student in the class is: (i)at most 60 kg (ii)at least 36 kg (iii)not more than 50kg. Also define two events in this context, one having probability 0 and the other having probability 1.
To solve the problem step-by-step, we will calculate the probabilities for the given weight conditions and define the events with probabilities of 0 and 1.
Step 1: Calculate the total number of students
The total number of students is given as 38.
Step 2: Calculate the probability that the weight of a student is at most 60 kg
To find the number of students whose weight is at most 60 kg, we need to sum the frequencies of the weight classes from 31-35 kg to 56-60 kg.
- Weight class 31-35 kg: 9 students
- Weight class 36-40 kg: 5 students
- Weight class 41-45 kg: 14 students
- Weight class 46-50 kg: 3 students
- Weight class 51-55 kg: 1 student
- Weight class 56-60 kg: 2 students
Total students at most 60 kg = 9 + 5 + 14 + 3 + 1 + 2 = 34 students
Now, we can calculate the probability:
P(at most 60 kg)=Number of students at most 60 kgTotal number of students=3438
Step 3: Calculate the probability that the weight of a student is at least 36 kg
To find the number of students whose weight is at least 36 kg, we sum the frequencies of the weight classes from 36-40 kg to 71-75 kg.
- Weight class 36-40 kg: 5 students
- Weight class 41-45 kg: 14 students
- Weight class 46-50 kg: 3 students
- Weight class 51-55 kg: 1 student
- Weight class 56-60 kg: 2 students
- Weight class 61-65 kg: 2 students
- Weight class 66-70 kg: 1 student
- Weight class 71-75 kg: 1 student
Total students at least 36 kg = 5 + 14 + 3 + 1 + 2 + 2 + 1 + 1 = 29 students
Now, we can calculate the probability:
P(at least 36 kg)=Number of students at least 36 kgTotal number of students=2938
Step 4: Calculate the probability that the weight of a student is not more than 50 kg
To find the number of students whose weight is not more than 50 kg, we sum the frequencies of the weight classes from 31-35 kg to 46-50 kg.
- Weight class 31-35 kg: 9 students
- Weight class 36-40 kg: 5 students
- Weight class 41-45 kg: 14 students
- Weight class 46-50 kg: 3 students
Total students not more than 50 kg = 9 + 5 + 14 + 3 = 31 students
Now, we can calculate the probability:
P(not more than 50 kg)=Number of students not more than 50 kgTotal number of students=3138
Step 5: Define two events
1. Event with Probability 0: The event that a student's weight is less than 31 kg. Since all the weights start from 31 kg, this event has a probability of 0.
2. Event with Probability 1: The event that a student's weight is at least 31 kg. Since all students have weights starting from 31 kg, this event has a probability of 1.
Summary of Results
- P(at most 60 kg)=3438
- P(at least 36 kg)=2938
- P(not more than 50 kg)=3138
- Event with Probability 0: Weight < 31 kg
- Event with Probability 1: Weight ≥ 31 kg
The total number of students is given as 38.
To find the number of students whose weight is at most 60 kg, we need to sum the frequencies of the weight classes from 31-35 kg to 56-60 kg.
- Weight class 36-40 kg: 5 students
- Weight class 41-45 kg: 14 students
- Weight class 46-50 kg: 3 students
- Weight class 51-55 kg: 1 student
- Weight class 56-60 kg: 2 students
P(at most 60 kg)=Number of students at most 60 kgTotal number of students=3438
To find the number of students whose weight is at least 36 kg, we sum the frequencies of the weight classes from 36-40 kg to 71-75 kg.
- Weight class 41-45 kg: 14 students
- Weight class 46-50 kg: 3 students
- Weight class 51-55 kg: 1 student
- Weight class 56-60 kg: 2 students
- Weight class 61-65 kg: 2 students
- Weight class 66-70 kg: 1 student
- Weight class 71-75 kg: 1 student
P(at least 36 kg)=Number of students at least 36 kgTotal number of students=2938
To find the number of students whose weight is not more than 50 kg, we sum the frequencies of the weight classes from 31-35 kg to 46-50 kg.
- Weight class 36-40 kg: 5 students
- Weight class 41-45 kg: 14 students
- Weight class 46-50 kg: 3 students
P(not more than 50 kg)=Number of students not more than 50 kgTotal number of students=3138
1. Event with Probability 0: The event that a student's weight is less than 31 kg. Since all the weights start from 31 kg, this event has a probability of 0.
2. Event with Probability 1: The event that a student's weight is at least 31 kg. Since all students have weights starting from 31 kg, this event has a probability of 1.
- P(at most 60 kg)=3438
- P(at least 36 kg)=2938
- P(not more than 50 kg)=3138
- Event with Probability 0: Weight < 31 kg
- Event with Probability 1: Weight ≥ 31 kg
Topper's Solved these Questions
Similar Questions
The distribution below gives the weight of 30 students in a class. Find the median weight of students: Weight (in kg): 40-45 45-50 50-55 55-60 60-65 65-70 70-75 No. of students: 2 3 8 6 6 3 2
View SolutionFollowing table shows the marks scored by a group of 90 students in a mathematics test of 100 marks. Marks 0-20 20-30 30-40 40-50 50-60 60-70 70-100 No. of Students: 7 10 10 20 20 15 8 Find the probability that marks scored by a student in the class is: at most 60 marks (ii) at least 60 marks (iii)not more than 50 marks
View SolutionFind the mean of the frequency distribution:
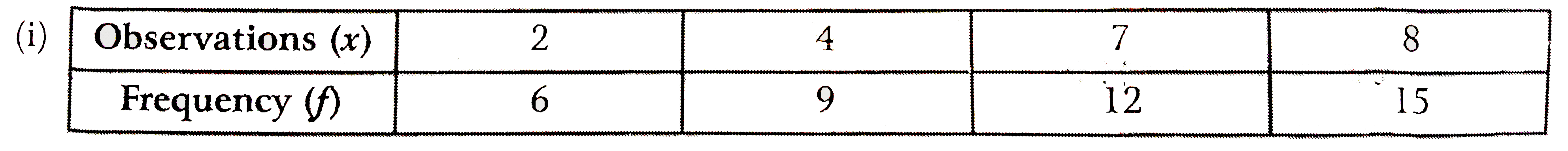
(ii) The weight of 40 students of class IX are given below:
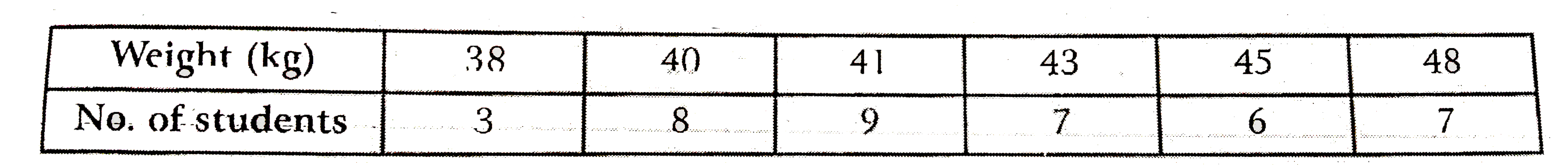 View Solution
View SolutionConsider the frequency distribution table (Table 14.3, Example 4, Chapter 14), which gives the weights of 38 students of a class. (i) Find the probability that the weight of a student in the class lies in the interval 46-50 kg.(ii) Give two events in this context, one having probability 0 and the other having probability 1.
View SolutionCalculate the mean, median and standard deviation of the following distribution: Class interval 31-35 36-40 41-45 46-50 51-55 56-60 61-65 66-70 Frequency: 2 3 8 12 16 5 2 3
View SolutionThe following is the distribution of weights (in kg) of 50 persons: Weight (in kg) 50-55 55-60 60-65 65-70 70-75 75-80 80-85 85-90 No. of Person 12 8 5 4 5 7 6 3 Draw a histogram for the above data.
View SolutionThe mean weight of 60 students in a class is 40 kg. The mean weight of boys is 50 kg while that of girls is 30 kg. Find the number of boys and girls in the class.
View SolutionThe mean weight of 150 students in a certain class is 60 kg. The mean weight of boys is 70 kg and that of girls in the class is 55 kg. Find the number of boys and girls in the class.
View SolutionThe weight (in kg) of students of a class are: Find the mode and median of this data. Is there more than one mode?
View SolutionFind the mean of the following frequency distributions: Class interval: 25-35 35-45 45-55 55-65 65-75 Frequency: 6 10 8 12 4
View Solution

