For a certain distribution, mode and median were found to be 1000 and 1250 respectively. Find mean for this distribution using an empirical relation
The correct Answer is:1375
To find the mean of the distribution using the empirical relation between the mode, median, and mean, we can follow these steps:
1. Identify the given values:
- Mode (Mo) = 1000
- Median (Me) = 1250
2. Use the empirical relation:
The empirical relation between mode, median, and mean (M) is given by:
3×Median=Mode+2×Mean
Rearranging this relation to find the mean gives:
Mean=3×Median−Mode2
3. Substitute the values into the equation:
Substitute the values of median and mode into the equation:
Mean=3×1250−10002
4. Calculate the numerator:
First, calculate 3×1250:
3×1250=3750
Now substitute this back into the equation:
Mean=3750−10002
5. Perform the subtraction:
Now calculate 3750−1000:
3750−1000=2750
6. Divide by 2:
Finally, divide by 2 to find the mean:
Mean=27502=1375
7. Conclusion:
Thus, the mean of the distribution is:
Mean=1375
Final Answer:
The mean for this distribution is 1375.
- Mode (Mo) = 1000
- Median (Me) = 1250
The empirical relation between mode, median, and mean (M) is given by:
3×Median=Mode+2×Mean
Rearranging this relation to find the mean gives:
Mean=3×Median−Mode2
Substitute the values of median and mode into the equation:
Mean=3×1250−10002
First, calculate 3×1250:
3×1250=3750
Now substitute this back into the equation:
Mean=3750−10002
Now calculate 3750−1000:
3750−1000=2750
Finally, divide by 2 to find the mean:
Mean=27502=1375
Thus, the mean of the distribution is:
Mean=1375
The mean for this distribution is 1375.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Short Answer Questions5videos
STATISTICS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions4videos
STATISTICS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - EXERCISE 14 E5videos
STATISTICS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Long Answer Questions5videos
SOME APPLICATIONS OF TRIGONOMETRY
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Revision Exercise Long Questions1videos
TRIANGLES
Similar Questions
Find the mean for the following distribution :
 View Solution
View SolutionFind the mean for the following distribution :
 View Solution
View SolutionFind mean of the following distribution using short cut method:
 View Solution
View SolutionFind the median for the following distribution :
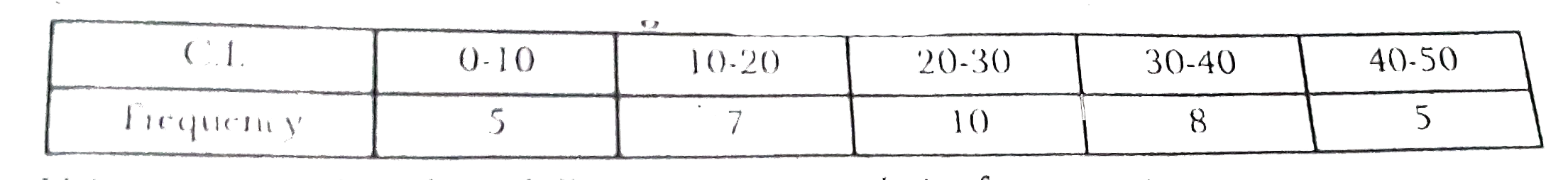 View Solution
View SolutionFor a slightly asymmetric distribution, mean and medain are 5 and 6, respectively. What is its mode ?
View SolutionFind the mean of the following distribution:
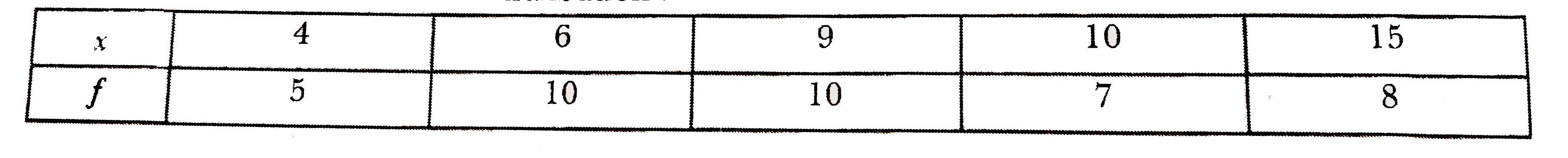 View Solution
View SolutionFind the mean of the following distribution:
 View Solution
View SolutionFind the mean of the following distribution :
 View Solution
View SolutionIf mode and mean of data are found 28 and 24 respectively, find median using empirical formula.
View SolutionFind the mode for the following distribution.
 View Solution
View Solution

