For all real numbers s,t,u and v such that s+t +u = 29 and s < v, which of the following statement is true ?
s+t+vlt29
t+u+v gt29
s+t+v=29
s+t+v=29
The correct Answer is:D
To solve the problem, we need to analyze the given conditions and check which of the statements is true based on those conditions.
1. Write down the given equation and inequality:
We have two conditions:
- Equation: s+t+u=29
- Inequality: s<v
2. Express s in terms of t and u:
From the equation s+t+u=29, we can isolate s:
s=29−t−u
3. Substitute s into the inequality:
Now, we substitute s in the inequality s<v:
29−t−u<v
4. Rearrange the inequality:
To isolate v, we can rearrange the inequality:
29<v+t+u
This can be rewritten as:
t+u+v>29
5. Identify the correct option:
Now, we compare our derived inequality t+u+v>29 with the options given in the question:
- Option 1: s+t+v<29
- Option 2: t+u+v>29 (This matches our derived inequality)
- Option 3: s+t+v=29
- Option 4: s+t+v>29
The correct statement is Option 2: t+u+v>29.
Conclusion:
Thus, the true statement among the options provided is:
Option 2: t+u+v>29.
We have two conditions:
- Equation: s+t+u=29
- Inequality: s<v
From the equation s+t+u=29, we can isolate s:
s=29−t−u
Now, we substitute s in the inequality s<v:
29−t−u<v
To isolate v, we can rearrange the inequality:
29<v+t+u
This can be rewritten as:
t+u+v>29
Now, we compare our derived inequality t+u+v>29 with the options given in the question:
- Option 1: s+t+v<29
- Option 2: t+u+v>29 (This matches our derived inequality)
- Option 3: s+t+v=29
- Option 4: s+t+v>29
Thus, the true statement among the options provided is:
Option 2: t+u+v>29.
Topper's Solved these Questions
Similar Questions
Let P(x)=x2+ax+b be a quadratic polynomial with real coefficients. Suppose there are real numbers s≠t such that P(s) = t and P(t) = s. Prove that b - st is a root of the equation x2+ax+bst=0.
View SolutionGraphs: s vs t, v vs t and a vs t
View SolutionIn Figure, PQRS is a quadrilateral and T and U are respectively points on PS and RS such that PQ=RQ, ∠PQT=∠RQU and ∠TQS=∠UQS. Prove that QT=QU.
View SolutionIf p,q,r,s,t are numbers such that p+q<r+s q+r<s+t r+s<t+p s+t<p+q thn the largest and smallest numbers are
View SolutionIf t=s−3, what is s+t?
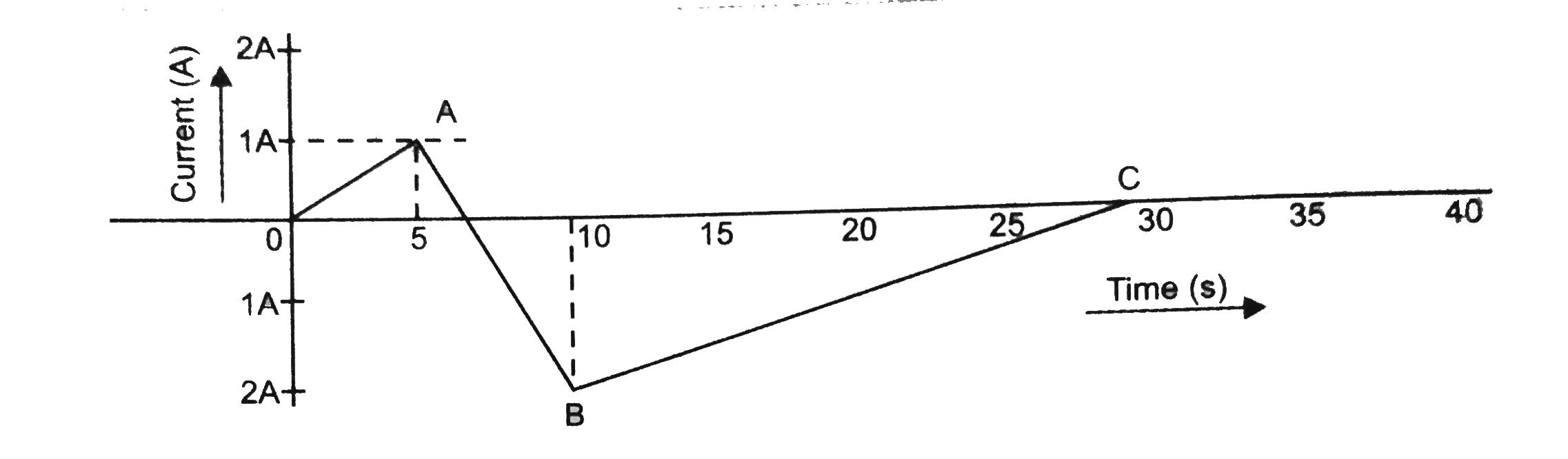
View SolutionA (current vs time) graph of the current passing through a solenoid is shown in Fig. For which time is the back electromotive force (u) a maximum? If the back emf t = 3 s is e, find the back emf at t = 7 s, 15 s and 40 s OA, AB and BC are straight line segments.
View Solutionsλt=ts+st for all inntegers s ant t. What is the value of 2λ16?
View SolutionLet S be the set of all real numbers. Then the relation R=
{(a,b):1+ab>0} on S is
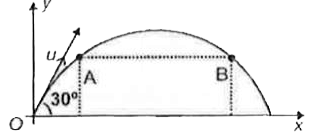
View SolutionA particle is thrown with a velocity of u m/s. it passes A and B as shown in figure at time t1=1 s andt2=3 s . The value of u is (g = 10 m/s2)
View SolutionLet A,B,C,D be (not necessarily ) real matrices such that AT=BCD,BT=CDA,CT=DABandDT=ABC for the matrix S=ABCD the least value of k such that Sk=S is
View Solution
