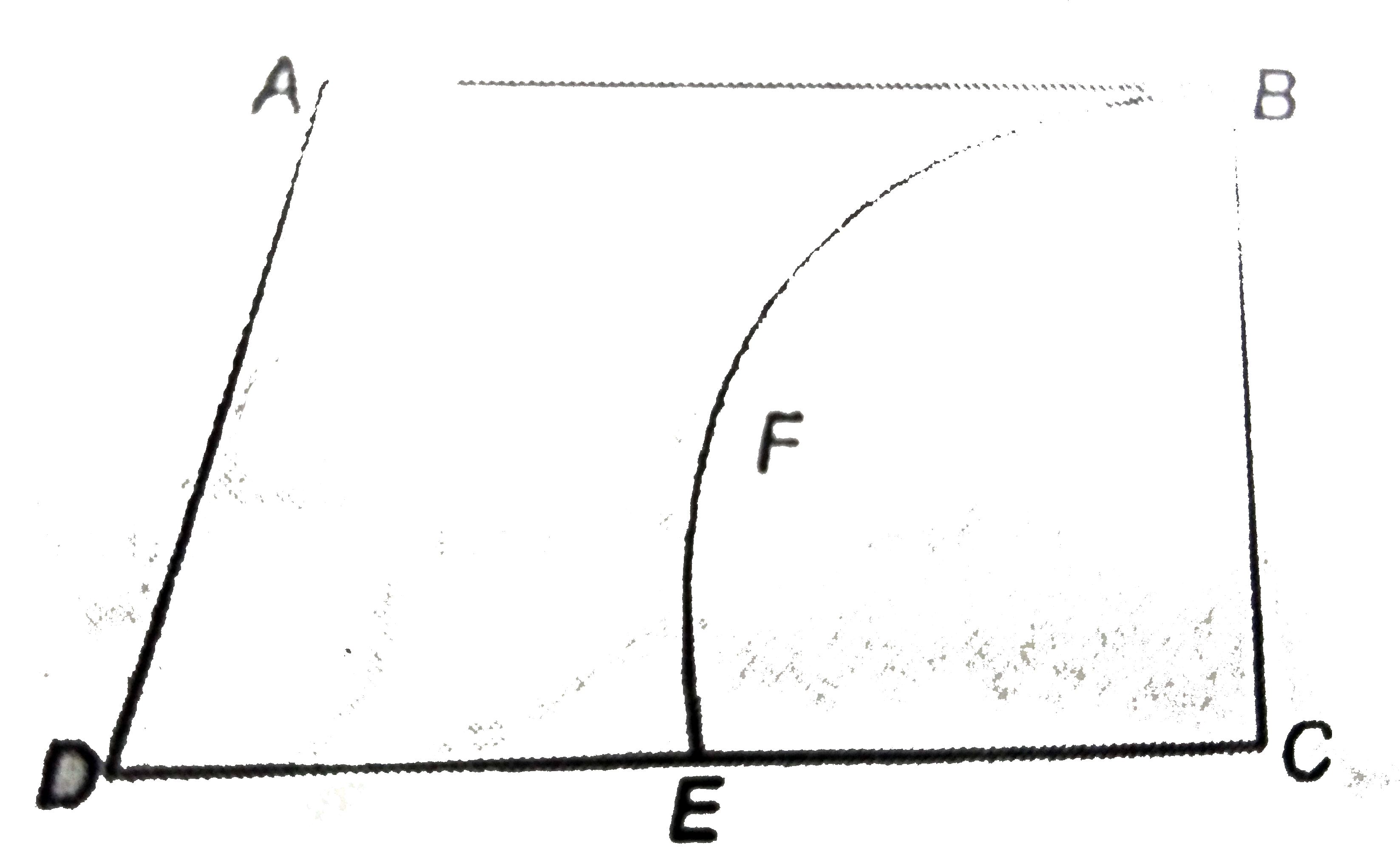
From a thin metallic piece in the shaped of a trapezium ABCD in which and ,a quarter circle BFEC is removed. Given, and calculate the area of remaining (shaded) part of metal sheet.

Given : and
Height of trapezium
bases of trapezium are AB and CD
As (radius of quarter circle)
Area of a trapezium ABCD =
Area of a trapezium ABCD =
Area of quarter circle =
Area of quarter circle =
Area of shaded part = Area of a trapezium ABCD - Area of quarter circle
Area of shaded part =
Topper's Solved these Questions
Similar Questions
From a thin metallic sheet in the shape of a trapezium ABCD in which AB∣∣CDand∠BCD=90∘, a quarter circle BFEC is removed. Given AB=BC=3.5cmandDE=2cm. Calculate the area of shaded region.
View SolutionFind the area of a trapezium ABCD in which AB∣∣DC,AB=77cm,BC=25cm,
CD=60cmandDA=26cm.
View Solution
Knowledge Check
Find the area of a trapezium ABCD in which AB || DC, AB = 26cm, BC = 25cm, CD = 40cm and DA = 25cm.
A648cm2B792cm2C660cm2D798cm2
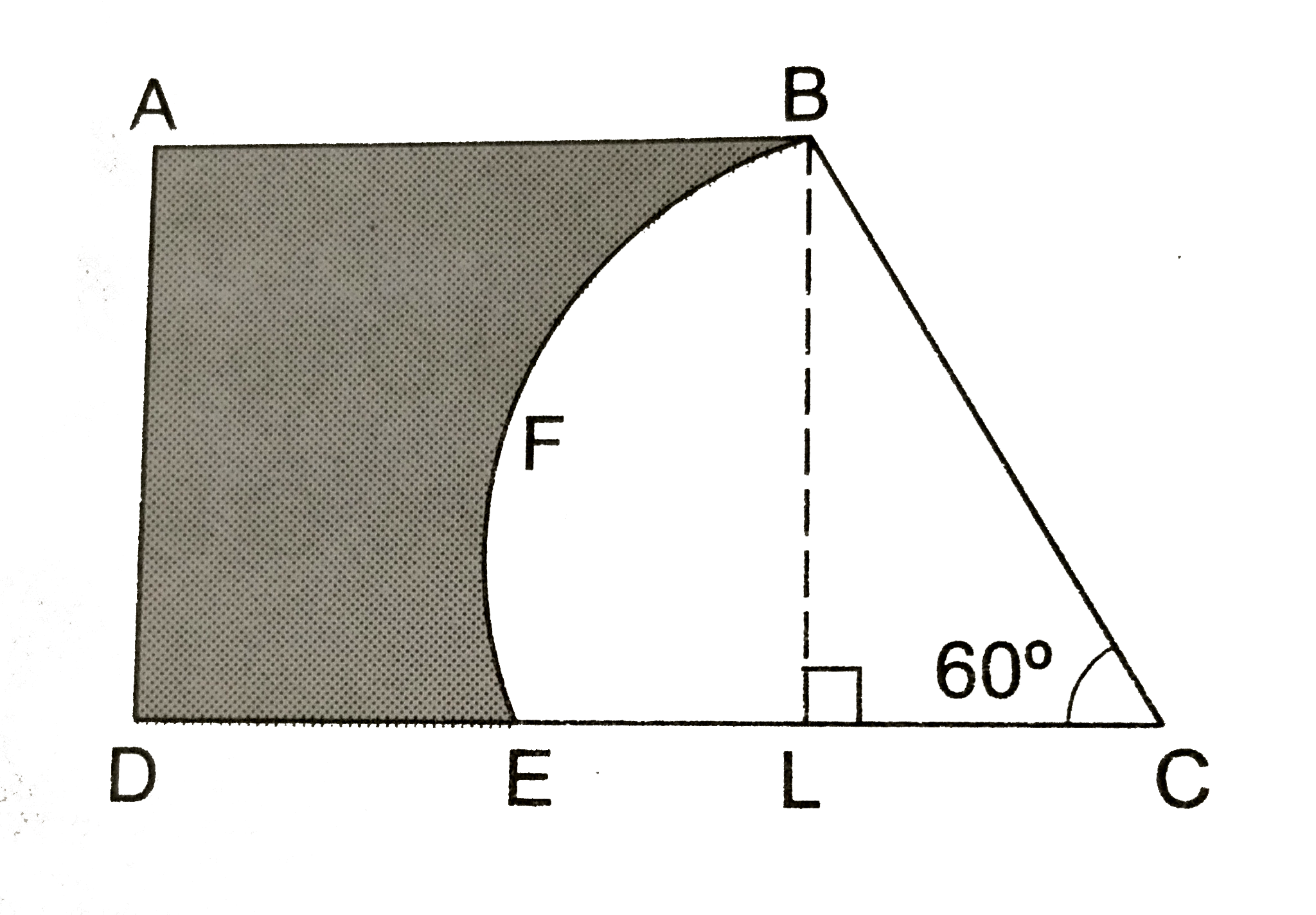
In the given figure, ABCD is a trapezium with AB∣∣CD nad ∠BCD=60∘.If BFEC is a sector of a circle with centre C and AB=BC=7 cm and DE=4cm, then find the area of the shaded region. [Use π=22/7 and √3=1.73]
View SolutionConstruct a trapezium ABCD in which AB∣∣CD,AB=8.2cm,BC=3.4cm,CD=3.4cm and∠B=75∘.
View SolutionCombination of quadrilateral and circle : In Figure; ABCD is a trapezium with AB||DC and ∠BCD=60∘. IF BFEC is a sector of a circle with centre C and AB = BC = 7cm and DE = 4cm. then find the area of shaded region
View SolutionIn the figure, ABCD is a trapezium with AB||DC, and ∠ABC=90∘. BCFE is a quadrant of a circle. If BC = CD = 4.2 cm and AE = 18 cm, find the area of the shaded region.
View SolutionIn the figure. AB and DC are parallel sides of a trapezium ABCD and angle ADC=90∘ given AB=15cm,CD=40cm and diagonal AC=41cm, calculate the area of trapezium ABCD
View SolutionConstruct a trapezium ABCD in which AB=7cm, BC=4cm, CD=3.2cm, ∠B=75∘ and DC∣∣AB.
View SolutionFind the area of a quadrilateral ABCD in which AB=3 cm, BC=4 cm, CD=4 cm, DA=5 cm and AC=5 cm.
View Solution
