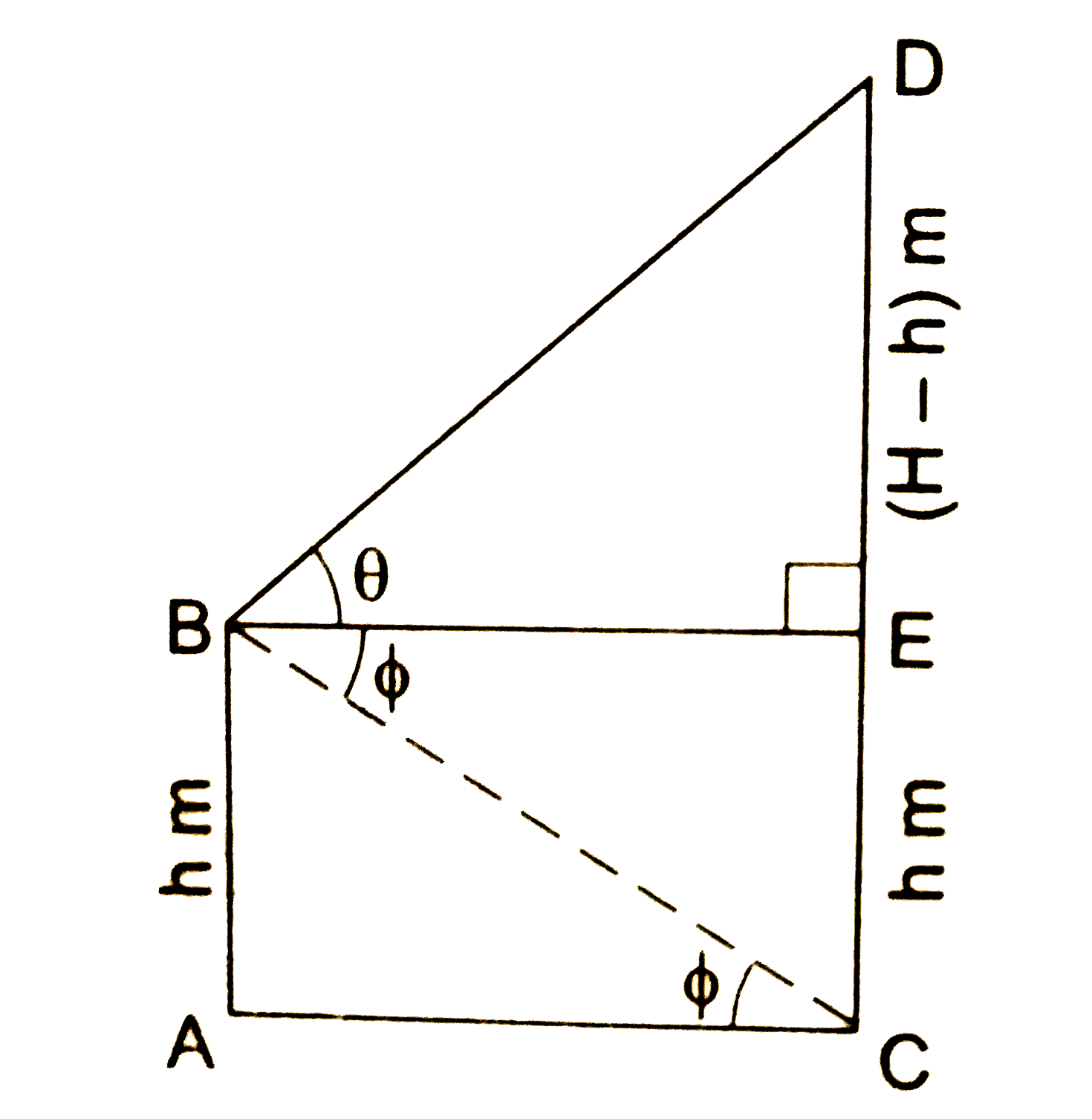
From a window (h metres high above the ground) of a house in a street, the angle of elevation and depression of the top and the foot of another house on the opposite side of the street are $θ$ and $ϕ$ respectively. Show that the height of the opposite house is $h (1 + tan θ cot ϕ)$ metres.

Video Solution

Text Solution

Verified by Experts

Let AB be the house with window at B and let the CD be the another house. Then, $A B = h$ metres.
Draw $B E ∣ ∣ A C$ , meeting $C D$ at E. Then,
$∠ E B D = θ$ and $∠ A C B = ∠ E B C = ϕ$ .
Let $C D = H$ metres. Then,
$C E = E B = h$ metres and
$E D = (H - h) m$ .
From right $Δ A C B$ , we have
$\frac{A C}{A B} = cot ϕ \Rightarrow \frac{A C}{h} = cot ϕ \Rightarrow A = h cot ϕ$ metres.
From right $Δ B E D$ , we have
$\frac{D E}{B E} = tan θ \Rightarrow \frac{(H - h)}{h cot ϕ} = tan θ [∵ B E = A C = h cot ϕ m]$
$\Rightarrow (H - h) = h tan θ cot ϕ$ .
$\Rightarrow H = h (1 + tan θ cot ϕ)$
Hence, the height of the opposite house is $h (1 + tan θ cot ϕ)$ metres.

Updated on:21/07/2023

From a window (h m high above the ground) of a house in a street, the angle of elevation and depression of the top and the foot of another house on the opposite side to the street are and 0, respectively. Then, the height of the opposite house is
A $h cot θ cot ϕ$
B $h (cot θ cot ϕ + 1)$
C $h tan θ cot ϕ$
D $h (tan θ cot ϕ + 1)$
From the top of a house A in a street, the angles of elevation and depression of the top and foot of another house B on the opposite side of the street are $60^{\circ}$ and $45^{\circ}$ , respectively. If the height of house A is 36 m, then what is the height of house B? (Your answer should be nearest to an Integer.
A91 cm
B93 m
C94 m
D98 m