From an arbitrary point M(x,y) of the curve y=xm(m>0) perpendiculars MN and ML (x>0) are dropped onto the coordinate axes. What part of the area of the rectangle ONML does the area ONMO constitute ?
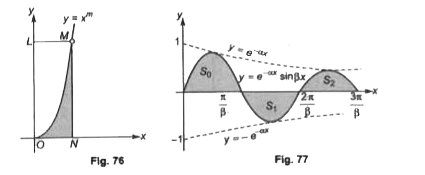
Step by step video & image solution for From an arbitrary point M(x,y) of the curve y= x^(m) (m gt 0) perpendiculars MN and ML (x gt 0) are dropped onto the coordinate axes. What part of the area of the rectangle ONML does the area ONMO constitute ? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Computing Areas with Parametrically Represented Boundaries7videos
APPLICATIONS OF THE DEFINITE INTEGRAL
- BOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - The Area of a Curvilinear Sector in Polar Coordinates5videos
APPLICATIONS OF THE DEFINITE INTEGRAL
- BOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Finding Average Values of a Function15videos
APPLICATIONS OF THE DEFINITE INTEGRAL
- BOOK - IA MARONCHAPTER - APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSEXERCISE - ADDITIONAL PROBLEMS9videos
APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONS
- BOOK - IA MARONCHAPTER - BASIC CLASSES OF INTEGRABLE FUNCTIONS EXERCISE - 5.8 INTEGRATION OF OTHER TRANSCENDENTAL FUNCTIONS5videos
BASIC CLASSES OF INTEGRABLE FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
The area bounded by the coordinate axes and the curve √x+√y=1 is
A1 square unitsB12 square unitsC13 square unitsD16 square units - Question 2 - Select One
The point M (x,y) of the graph of the function y=e−|x| so that area bounded by the tangent at M and the coordinate axes is greatest is
A(1,e−1)B(2,e−2)C(−2,e2)D(0,1) - Question 3 - Select One
The area bounded by the coordinate axes and the curve √x+√y=1, is
A1 square unitB12 square unitC13 square unitD16 square unit
A curve y=memx where m>0 intersects y-axis ai a point P,
What is the slope of the curve at the point of intersection P?View SolutionThe area bounded by the coordinate axes and normal to the curve y=logex at the point P( 1 , 0), is
View SolutionA circle touches both the coordinate axes and the line x−y=√2a,a>0, the coordinates of the centre of the circle cannot be
View SolutionThe area of the traingle formed by the coordinate axes and a tangent to the curve xy=a2 at the point (x1,y1) is
View SolutionDistance of point P on the curve y=x3/2 which is nearest to the point M (4, 0) from origin is
View Solution

