A circle touches both the coordinate axes and the line x−y=√2a,a>0, the coordinates of the centre of the circle cannot be

A

(a, a)

B

(a, -a)

C

(-a, a)

D

(-a, -a)

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B

Let the radius of the circle be r. Then, coordinates of its centre can be (r, r), (-r, -r) and (r, -r).
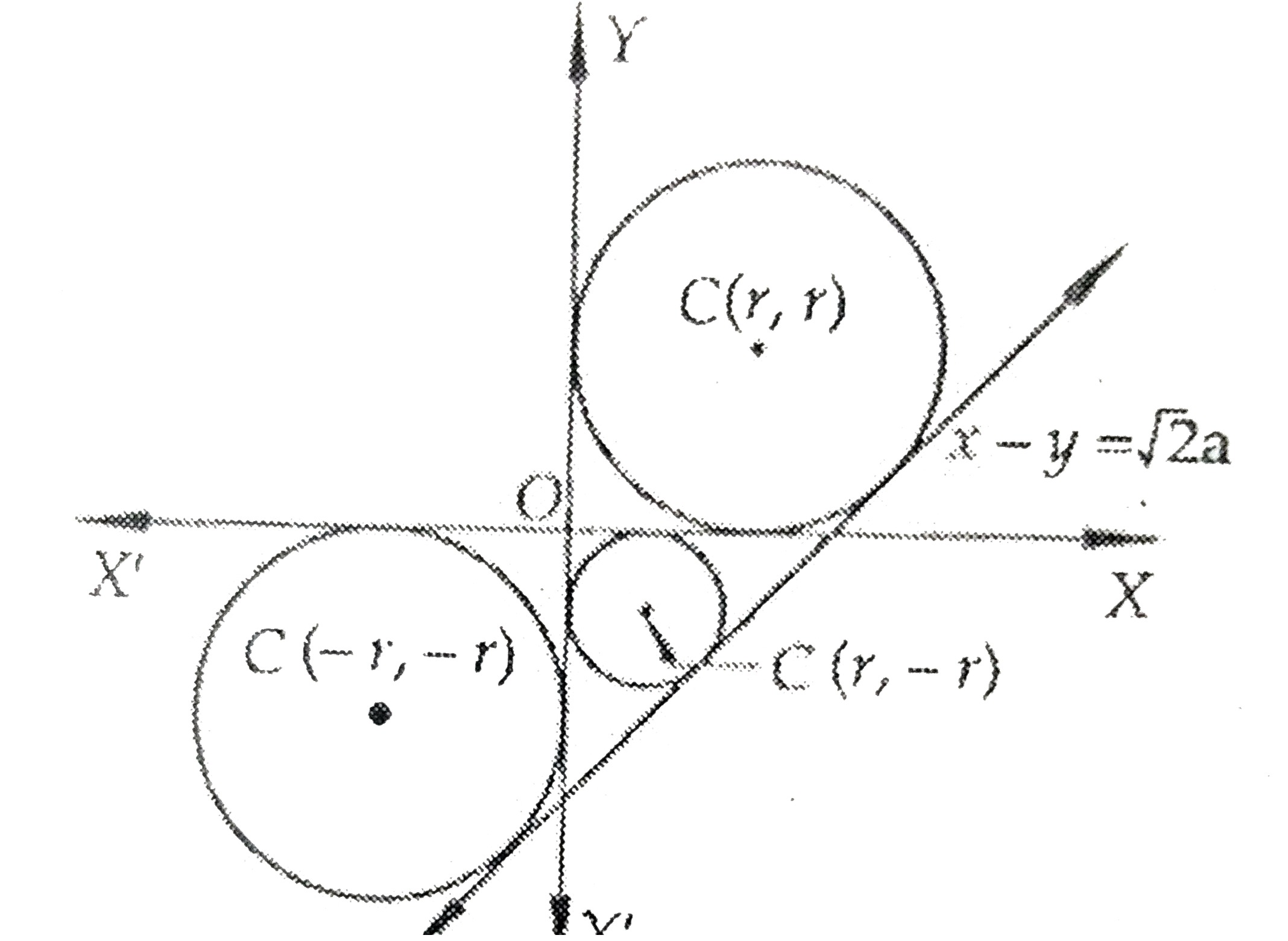
ocr_image
The circle touches x−y=√2a
∴∣∣∣−√2a√2∣∣∣=r when centre is at (r, r) or (-r, -r)
and ∣∣∣2r−√2a√2∣∣∣=r when centre is at (r, -r)
⇒r=aandr=(√2±1)a

Updated on:21/07/2023
|
Class 12MATHSCIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The circle that can be drawn to touch the coordinate axes and the line 4x+3y=12 cannot lie in

    Afirst quadrant
    Bsecond quadrant
    Cthird quadrant
    Dfourth quadrant

  • Find the coordinates of the centre of the circle x2+y2−8x−4y=5.

    A(2,4)
    B(−2,4)
    C(4,2)
    D(4,−2)

  • A circle touches the x-axis and also touches the circle with centre (0,3) and radius 2. The locus of the centre of the circle is :

    Aa circle
    Ban ellipse
    Ca parabola
    Da hyperbola