From the external point P tangents PA and PB are drawn to a circle with centre O. If , then find .
To solve the problem, we need to find the angle ∠AOB given that ∠PAB=50∘ where PA and PB are tangents drawn from an external point P to a circle with center O.
1. Draw the Diagram:
- Draw a circle and label its center as O.
- Mark an external point P.
- Draw tangents PA and PB from point P to the points A and B on the circle.
2. Identify Given Information:
- We know that ∠PAB=50∘.
3. Use the Property of Tangents:
- Since PA and PB are tangents from the same external point P, we have PA=PB.
- By the property of tangents, the angles opposite to equal sides are equal. Therefore, ∠PAB=∠PBA.
4. Calculate ∠PBA:
- Since ∠PAB=50∘, it follows that ∠PBA=50∘.
5. Apply the Angle Sum Property in Triangle PAB:
- The sum of angles in triangle PAB is 180∘.
- Therefore, we can write:
∠PAB+∠PBA+∠APB=180∘
- Substituting the known values:
50∘+50∘+∠APB=180∘
- This simplifies to:
100∘+∠APB=180∘
- Thus, ∠APB=180∘−100∘=80∘.
6. Use the Quadrilateral Property:
- In quadrilateral OAPB, the sum of opposite angles is 180∘.
- Therefore, we have:
∠AOB+∠APB=180∘
- Substituting ∠APB:
∠AOB+80∘=180∘
- Rearranging gives:
∠AOB=180∘−80∘=100∘
Final Answer:
∠AOB=100∘
- Draw a circle and label its center as O.
- Mark an external point P.
- Draw tangents PA and PB from point P to the points A and B on the circle.
- We know that ∠PAB=50∘.
- Since PA and PB are tangents from the same external point P, we have PA=PB.
- By the property of tangents, the angles opposite to equal sides are equal. Therefore, ∠PAB=∠PBA.
- Since ∠PAB=50∘, it follows that ∠PBA=50∘.
- The sum of angles in triangle PAB is 180∘.
- Therefore, we can write:
∠PAB+∠PBA+∠APB=180∘
- Substituting the known values:
50∘+50∘+∠APB=180∘
- This simplifies to:
100∘+∠APB=180∘
- Thus, ∠APB=180∘−100∘=80∘.
- In quadrilateral OAPB, the sum of opposite angles is 180∘.
- Therefore, we have:
∠AOB+∠APB=180∘
- Substituting ∠APB:
∠AOB+80∘=180∘
- Rearranging gives:
∠AOB=180∘−80∘=100∘
∠AOB=100∘
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - PRACTICE - TEST (SECTION - B)2videos
CIRCLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - PRACTICE - TEST (SECTION - C)2videos
CIRCLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - LONG ANSWER TYPE QUESTIONS2videos
CIRCLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ARITHMETIC PROGRESSION EXERCISE - PRACTICE TEST (SECTION D)1videos
ARITHMETIC PROGRESSION
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - Co-ordinate GeometryEXERCISE - PRACTICE-TEST (Coordinate Geometry) SECTION-D1videos
Co-ordinate Geometry
Similar Questions
In From an external point P, Two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O . If ∠QPR=90∘ then length of PQ is
 View Solution
View SolutionFrom an external point P, two tangents, PA and PB are drawn to a circle with centre 0. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA=10 cm, find the perimeter of the triangle PCD.
View Solution
Knowledge Check
- Question 1 - Select One
Two tangents PA and PB are drawn to a circle with centre O from an external point P. If ∠OAB=30∘, then ∠APB is:
केंद्र O वाले वृत्त पर एक बाहरी बिंदु P से दो स्पर्श रेखाएँ PA तथा PB खींची जाती हैं | यदि ∠OAB=30∘ है, तो ∠APB का मान क्या होगा ?A15∘B30∘C120∘D60∘ - Question 2 - Select One
From a point P two tangents PA and PB are drawn to a circle with centre O.if OP is equal to diameter of the circle then ∠APB is
A60∘B45∘C90∘D30∘ - Question 3 - Select One
If PA and PB are tangents to the circle with centre O such that ∠APB=50∘ then ∠OAB is equal to
A50∘B30∘C40∘D25∘
From an external point P , tangents PA and PB drawn to a circle with centre O . If CD is the tangent to the circle at a point E and PA=14cm , find the perimeter of PCD .
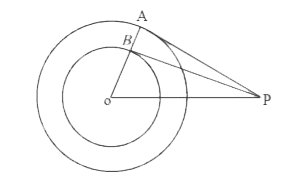
View SolutionTwo concentric circle with centre O are of radii 6 cm and 3 cm. From an external point P, tangents PA and PB are drawn to these circle as shown in the figure. If AP = 10 cm. Find BP
 View Solution
View SolutionIn the figure, PA is a tangent from an external point P to a circle with centre O. If ∠POB=115∘, find ∠APO.
 View Solution
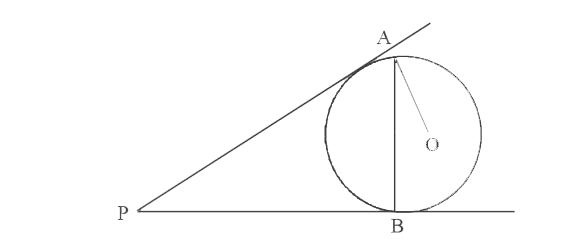
View SolutionTwo tangents PA and PB are drawn to a circle with centre O from an external point P. Prove that ∠APB=2∠OAB
 View Solution
View SolutionFrom a point P, two tangents PA and PB are drawn to a circle with centre O. If OP is equal to diameter of the circle, then ∠APBis
View Solution

