From the following data, using mean, calculate mean deviation and the coefficient of mean deviation.
15, 17, 19, 25, 30, 35, 48
The correct Answer is:M.D = 9.14, coefft. of M.D = 0.338
Step by step video, text & image solution for From the following data, using mean, calculate mean deviation and the coefficient of mean deviation. 15, 17, 19, 25, 30, 35, 48 by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - MEASURES OF DISPERSIONEXERCISE - EXERCISE 21 (b)19videos
MEASURES OF DISPERSION
- BOOK - ICSECHAPTER - MEASURES OF DISPERSIONEXERCISE - CHAPTER TEST6videos
MEASURES OF DISPERSION
- BOOK - ICSECHAPTER - MEASURES OF DISPERSIONEXERCISE - CHAPTER TEST6videos
MEASURES OF DISPERSION
- BOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCYEXERCISE - EXERCISE14videos
MEASURES OF CENTRAL TENDENCY
- BOOK - ICSECHAPTER - MOCK TEST PAPER-2021EXERCISE - SECTION - C10videos
MOCK TEST PAPER-2021
Similar Questions
From the following data, using mean, calculate mean deviation and the coefficient of mean deviation.
21, 23, 25, 28, 30, 32, 38, 39, 46, 48View SolutionFrom the following data, using mean, calculate mean deviation and the coefficient of mean deviation.
10, 70, 50, 53, 20, 95, 42, 60, 48, 80View SolutionFor the following, using median, calculate mean deviation and coefficient of mean deviation.
 View Solution
View SolutionFor the following, using median, calculate mean deviation and coefficient of mean deviation.
 View Solution
View SolutionFor the following, using median, calculate mean deviation and coefficient of mean deviation.
100, 150, 200, 250, 360, 490, 500, 600, 671View SolutionFor the following, calculate mean deviation and coefficient of mean deviation.
3, 9, 5, 3, 12, 10, 18, 4, 7, 19, 21View SolutionCalculate the mean deviation and coefficient of mean deviation for the following distribution:
 View Solution
View SolutionIf the mean deviation from the median is 15 and median is 450, then find the coefficient of mean deviation.
View SolutionFind the mean from the following table using step deviation method :
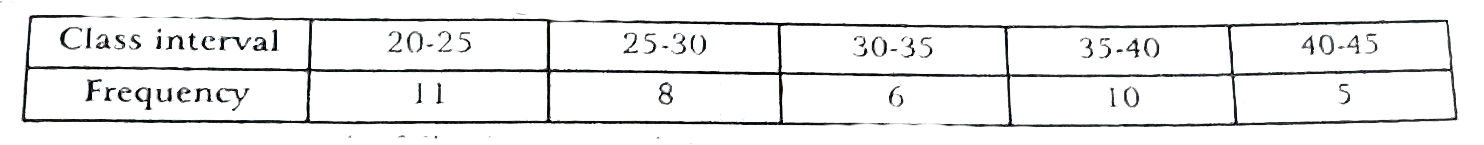 View Solution
View SolutionFind the mean from the following table using step deviation method :
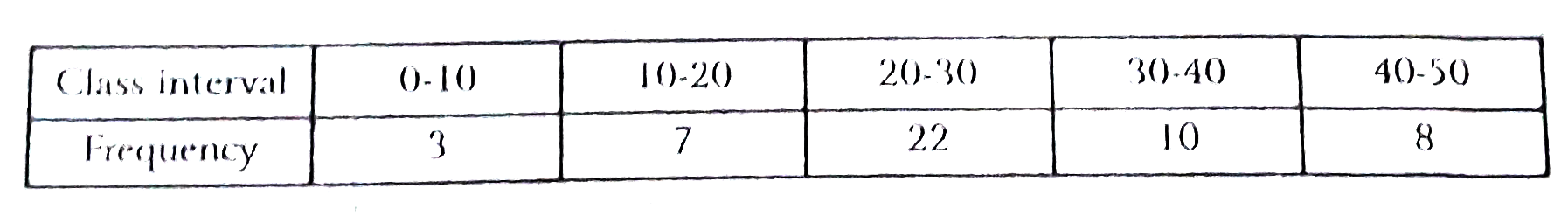 View Solution
View Solution
