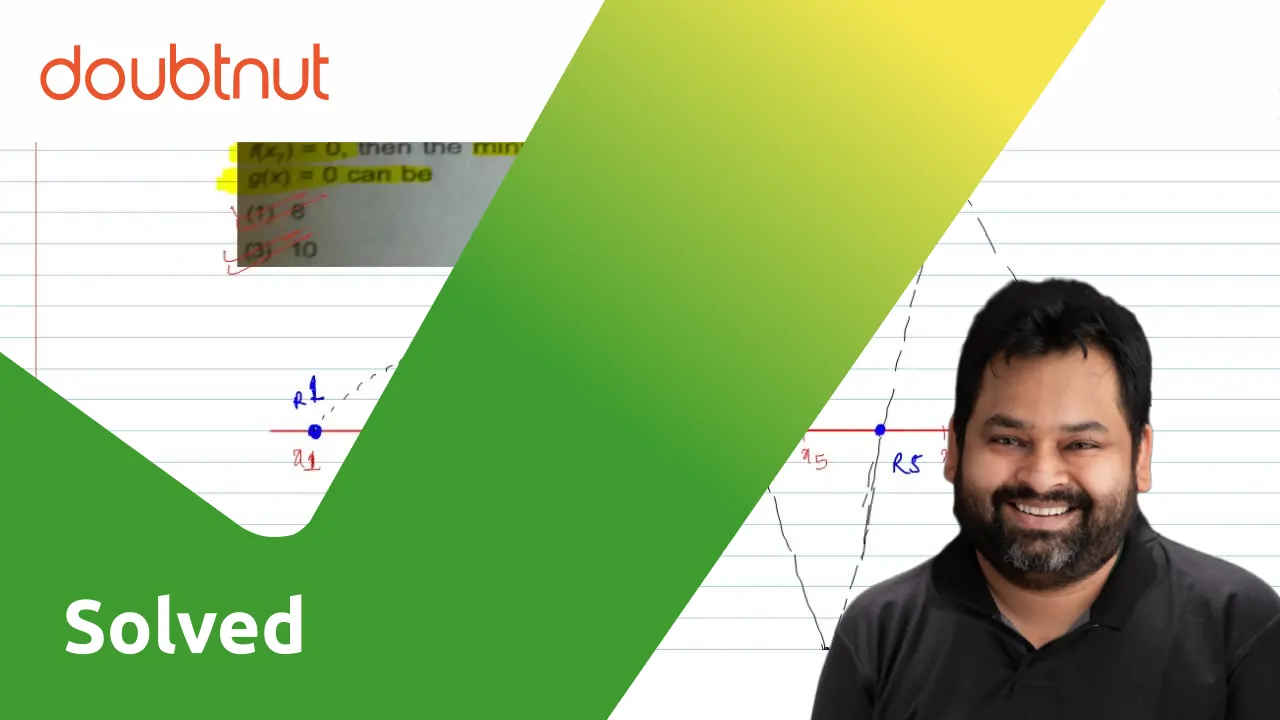
f(x) is a twice differentiable function and g(x) is defined as g(x)=(f'(x))2+f''(x)⋅f(x) on [x1,x2]. If x1<x2<x3<x4<x5<x6<x7,f(x1)=0,f(x2)=2,f(x3)=−3,f(x4)=4,f(x5)=−5,f(x6)andf(x7)=0, then the minimum number of real roots of g(x)=0 can be
Step by step video & image solution for f(x) is a twice differentiable function and g(x) is defined as g(x)=(fprime(x))^2+f prime prime(x)*f(x) on [x_1,x_2]. If x_1 < x_2 < x_3 < x_4 < x_5 < x_6 < x_7,f(x_1)=0,f(x_2)=2,f(x_3)=-3,f(x_4)=4,f(x_5)=-5,f(x_6) and f(x_7)=0, then the minimum number of real roots of g(x)=0 can be by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
The number of solutions to the system of equations x1+x2+x3+x4+x5=20 and x1+x2=15 wher xk≥0
03:03View SolutionLet f(x)=x1(−x) and ' a ' be a real number. If x0=a, x1=f(x0),x2=f(x1),x3=f(x2) and so on. If x2009=1, then the value of reciprocal of ' a ' is
Text SolutionView SolutionIf f(x)=log(1+x1−x),then (a)f(x1)f(x2)=f(x1+x2) (b)f(x+2)−2f(x+1)+f(x)=0 (c)f(x)+f(x+1)=f(x2+x) (d)f(x1)+f(x2)=f(x1+x21+x1x2)
05:20View SolutionIf f(x)=log(1+x1−x),then (a)f(x1)f(x)=f(x1+x2) (b)f(x+2)−2f(x+1)+f(x)=0 (c)f(x)+f(x+1)=f(x2+x) (d)f(x1)+f(x2)=f(x1+x21+x1x2)
03:55View SolutionLet f(x)=x1−x and ' a ' be a real number. If x0=a, x1=f(x0),x2=f(x1),x3=f(x2) and so on. If x2011=−(12012), then the value of reciprocal of ' a ' is
02:35View SolutionThe number of solutions to the system of equations x1+x2+x3+x4+x5=20 and x1+x2=15 wher xk≥0
02:44View SolutionIf f(x)=log((1+x)/(1-x)),t h e n (a) f(x_1)f(x_2)=f(x_1+x_2) (b) f(x+2)-2f(x+1)+f(x)=0 (c) f(x)+f(x+1)=f(x^2+x) (d) f(x_1)+f(x_2)=f((x_1+x_2)/(1+x_1x_2))
04:46View SolutionThe number of solutions to the system of equations x1+x2+x3+x4+x5=20 and x1+x2=15 wher xk≥0
04:32View Solution