Given A≡(1,1) and AB is any line through it cutting the x-axis at B. If AC is perpendicular to AB and meets the y-axis in C , then the equation of the locus of midpoint P of BC is
x+y=1
x+y=2
x+y=2xy
2x+2y=1
The correct Answer is:A
The equation of line AB is y-1 = m(x-1). Therefore, the equation of line AC is
y−1=−1m(x−1)
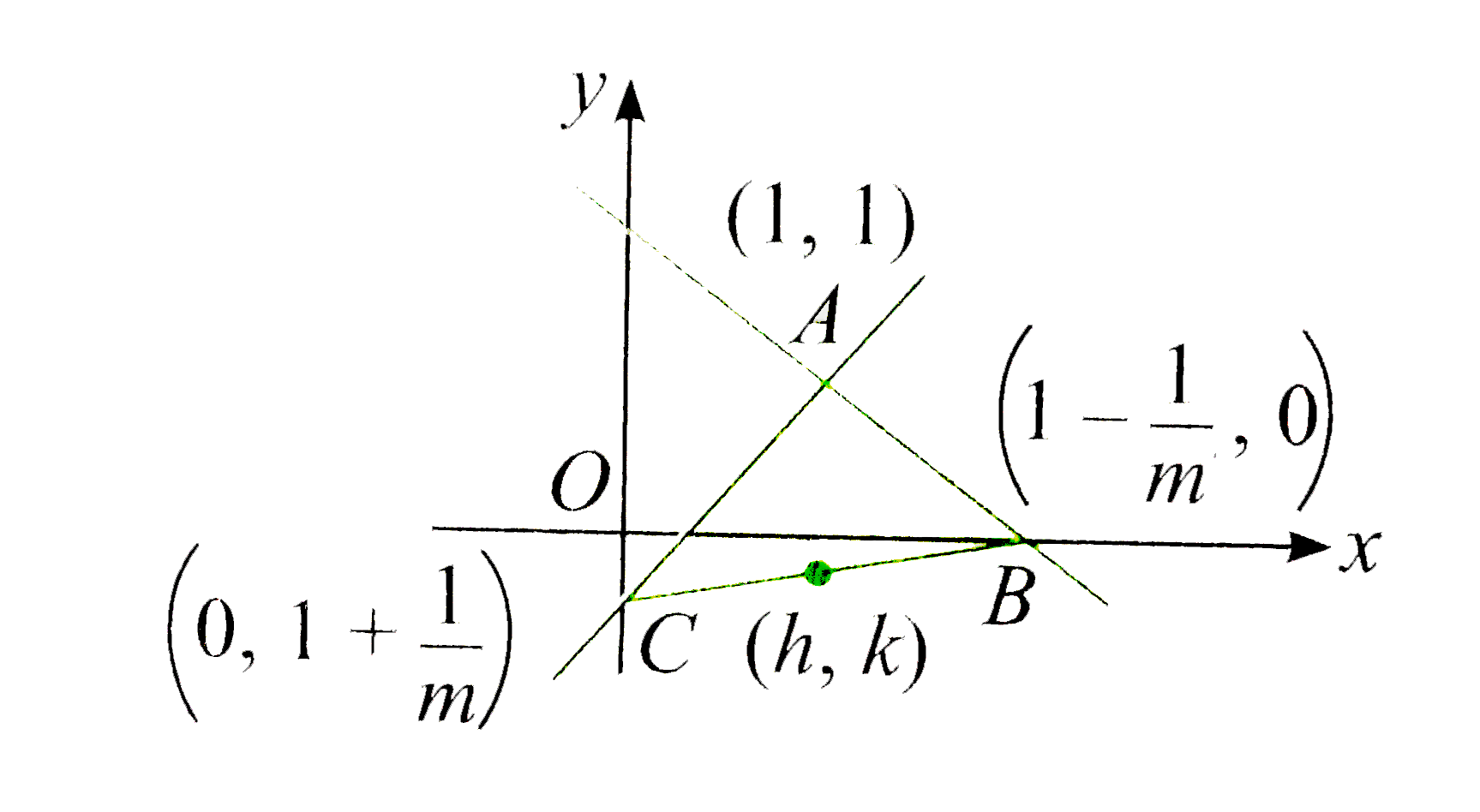
2h=1−1m
2k=1+1m
Eliminating m, we have locus x+y=1.
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Multiple)
30 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Comprehension)
27 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.6
5 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
A(0,6) and B(2t,0), where t is a parameter midpoint of A and B is M. perpendicular bisector of AB cuts y-axis at C then Find the locus of midpoint of MC
View SolutionThe line xa+yb=1 cuts the axes in A and B and a line perpendicular to AB cuts the axes in P and Q. Locus of the points of intersection of AQ and BP is x2+y2+ax+by=0.
View Solution
Knowledge Check
A straight line through the point (1,1) meets the x-axis at 'A' and the y axis at 'B'. The locus of the mid point of AB is :
A2xy + x + y = 0Bx + y - 2xy = 0Cx + y + 2 = 0Dx + y - 2 = 0A straight line through the point (1,1) meets the X-axis at A and Y-axis at B. The locus of the mid-point of AB is
A2xy+x+y=0Bx+y-2y=0Cx+y+2=0Dx+y-2=0Through the point P(3,4) a pair of perpendicular lines are dranw which meet x-axis at the point A and B. The locus of incentre of triangle PAB is
Ax2−y2−6x−8y+25=0Bx2+y2−6x−8y+25=0Cx2−y2+6x+8y+25=0Dx2+y2+6x+8y+25=0
A straight line is drawn through P(3,4) to meet the axis of x and y at AandB , respectively. If the rectangle OACB is completed, then find the locus of C.
View SolutionThe line 3x+2y=24 meets x - axis at B and the y -axis at A. The perpendicular bisector of AB meets the line through (0, -1) parallel to x -axis at C, then the area of the triangle ABC is_____
View SolutionThe plane x+y=0 (A) is parallel to y-axis (B) is perpendicular to z-axis (C) passes through y-axis (D) none of these
View SolutionA is any point on X-axis and B is any point of Y- axis and P is a variable point on AB with PA=b and PB=aand AB=a+b. Find the equation of locus of P
View SolutionEquation of the plane which passes through the Z-axis, and is perpendicular to the line
x−acosθ=y−bsinθ=z−c0 is
View Solution
