Given f(x) is a periodic function with period 2 and it is defined as
f(x)=⎧⎨⎩[cosπx2]+1,0<x<12−x,1≤x<2
Here [⋅] represents the greatest integer ≤x. If f(0)=1, then draw the graph of the function for x∈[−2,2]. Solution in Tamil
f(x)=⎧⎨⎩[cosπx2]+1,0<x<12−x,1≤x<2
={1,0<x<12−x,1≤x<2
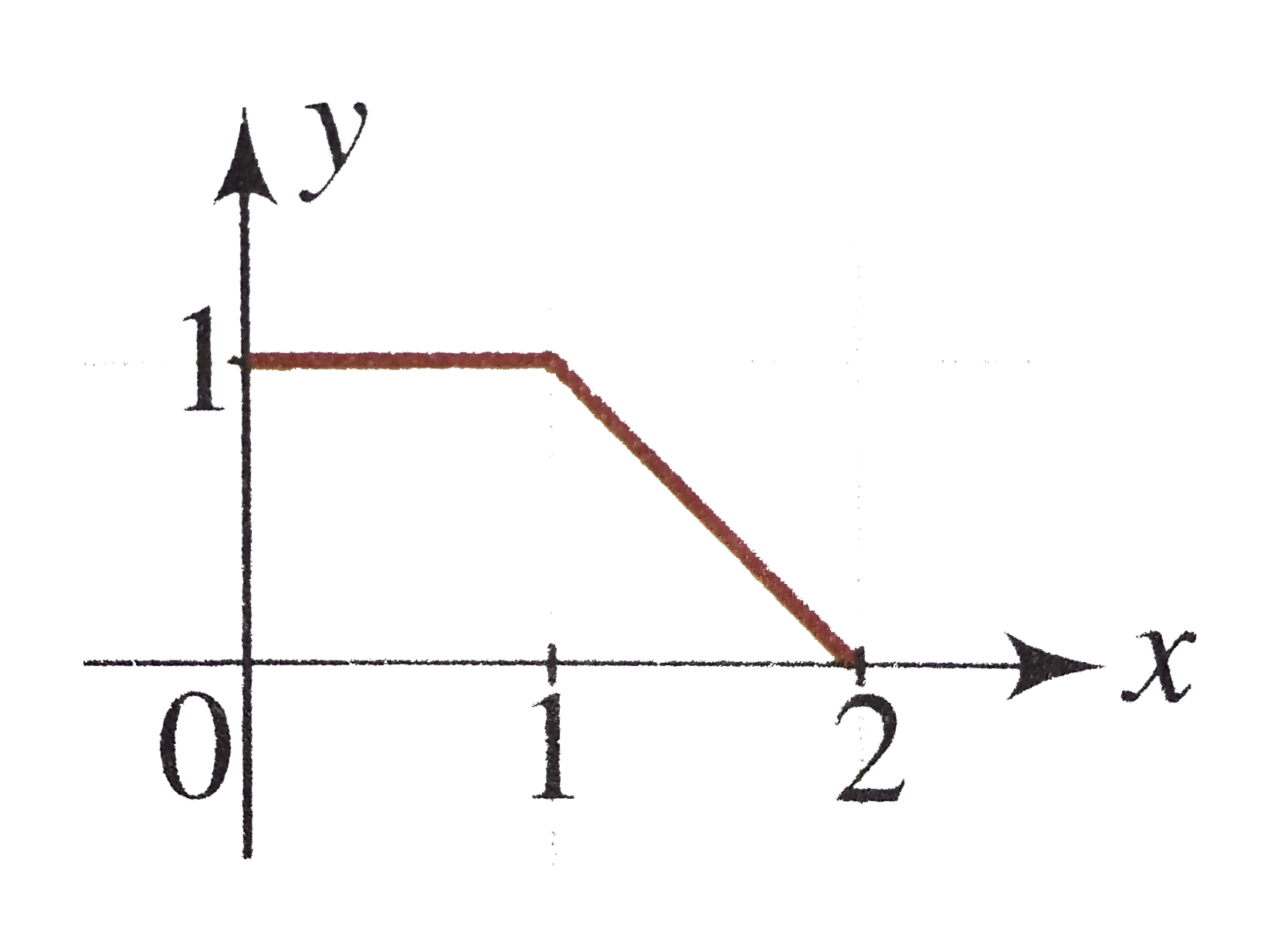
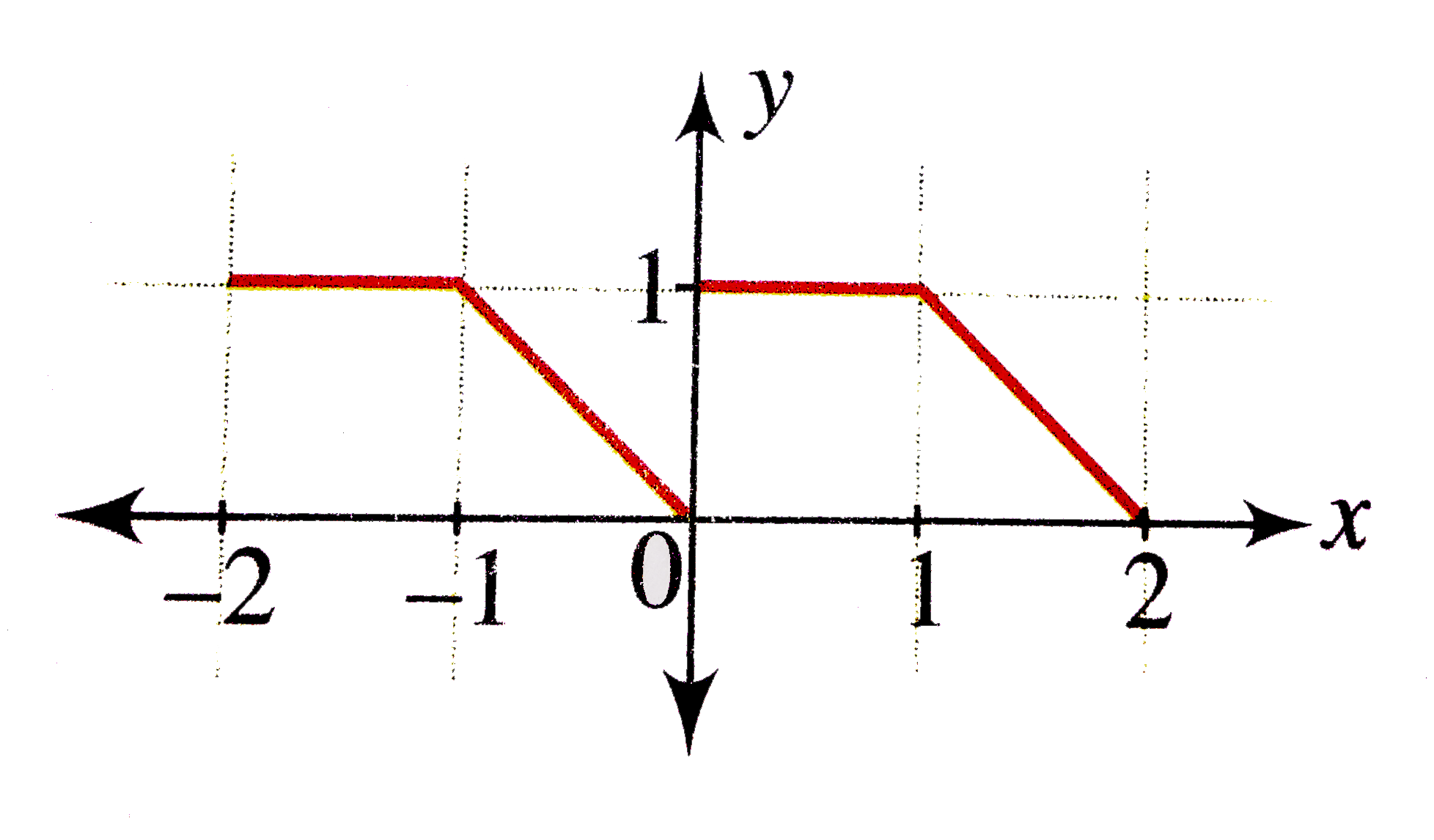
Since the function if periodic with period '2', the required graph for x∈[−2,1] is as follows.
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
4 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
Similar Questions
Draw the graph of y=1(1/x).
View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=0
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionGiven f(x) is a periodic function with period 2 and it is defined as
f(x)=⎧⎨⎩[cosπx2]+1,0<x<12−x,1≤x<2
Here [⋅] represents the greatest integer ≤x. If f(0)=1, then draw the graph of the function for x∈[−2,2].
View SolutionIf f(x)={∣∣1−4x2∣∣,0≤x<1[x2−2x],1≤x<2, where [] denotes the greatest integer function, then
View SolutionIf f(x)=⎧⎪⎨⎪⎩x, for 0≤x<12, for x=1x+1, for 1<x≤2, then f is
View SolutionIf the function f is defined by f(x)=⎧⎪⎨⎪⎩x+2,x>12,−1≤x≤1x−1,−3g<x<−1 then find the values of (i) f(3)
View SolutionIf the function f is defined by f(x)=⎧⎪⎨⎪⎩x+2,x>12,−1≤x≤1x−1,−3g<x<−1 then find the values of (ii) f(0)
View SolutionIf the function f is defined by f(x)=⎧⎪⎨⎪⎩x+2,x>12,−1≤x≤1x−1,−3<x<−1 then find the values of (iii) f(−1.5)
View SolutionIf the function f is defined by f(x)=⎧⎪⎨⎪⎩x+2,x>12,−1≤x≤1x−1,−3<x<−1 then find the values of (v) f(−5)
View SolutionLet f(x)=x2+1[x],1<x≤3.9.[.] denotes the greatest integer function. Then
View SolutionGiven f(x) is a periodic function with period 2 and it is defined as
f(x)=⎧⎨⎩[cosπx2]+1,0<x<12−x,1≤x<2
Here [⋅] represents the greatest integer ≤x. If f(0)=1, then draw the graph of the function for x∈[−2,2].
View Solutionf(x)=1+[cosx]x,0<x≤π/2 में जहाँ [] महत्तम पूर्णांक फलन है, तो यह-
View SolutionIf f(x)=x2+1[x], ([.] denotes the greatest integer function), 1≤x<4, then
View SolutionIf f(x)={:{(x", for " 0 le x lt 1),(2", for " x=1),(x+1", for " 1 lt x le 2):} , then f is
View Solution
