Given is a periodic function with period 2 and it is defined as
Here represents the greatest integer . If , then draw the graph of the function for .
Text Solution

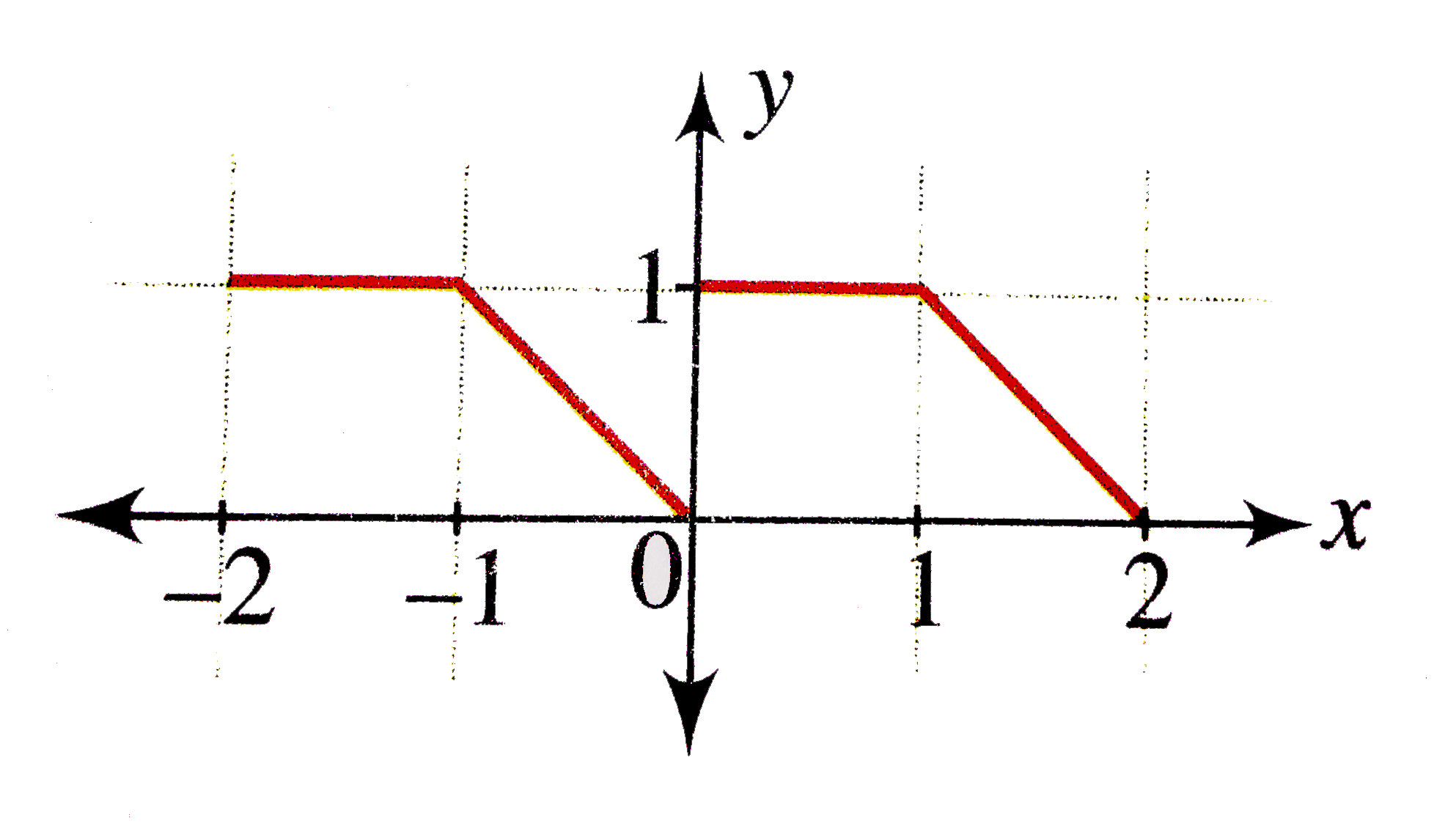
Since the function if periodic with period '2', the required graph for is as follows.
|
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise
13 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
Similar Questions
Knowledge Check
If f(x)={∣∣1−4x2∣∣,0≤x<1[x2−2x],1≤x<2, where [] denotes the greatest integer function, then
Af(x) is continuous for all x∈[0,2)Bf(x) is differentiable for all x∈[0,2)−{1}Cf(X) is differentiable for all x∈[0,2)−{12,1}DNone of theseIf f(x)={x[x]0≤x<2(x−1)[x]2≤x<3 where [.] denotes the greatest integer function, then
Aboth f'(1) and f'(2) do not existBf'(1) exist but f'(2) does not existCf'(2) exist but f'(1) does not existDboth f'(1) and f'(2) existIf a function f(x) is defined as f(x)=⎧⎪⎨⎪⎩−x,x<0x2,0≤x≤1x2−x+1,x>1 then
Af(x) is differentiable at x = 0 and x = 1Bf(x) is differentiable at x = 0 but not at x = 1Cf(x) is not differentiable at x = 1 but not at x = 0Df(x) is not differentiable at x = 0 and x = 1
f (x) is an even periodic function with period 10 in [0,5],f(x)=⎧⎪⎨⎪⎩2x0≤x<23x2−82≤x<410x4≤x≤5. Then:
View SolutionIf f(x)={x[x]0≤x<2(x−1)[x]2≤x<3 where [.] denotes the greatest integer function, then continutity and diffrentiability of f(x)
View Solutionf (x) is an even periodic function with period 10 In [0,5],f(x)=⎧⎪⎨⎪⎩2x0≤x<23x2−82≤x<410x4≤x≤5. Then:
View SolutionIf f(x)=⎧⎨⎩x, for 0≤x<121−x, for 12≤x<1 , then
View SolutionIf f(x)=cos(x2−4[x]) for 0<x<1, where [x] denotes the greatest integer ≤x, then f'(√π/2) is equal
View Solution
