Given tanα=512 , find other trigonometric ratios
Video Solution
Text Solution
We know that ,
tanθ=perpendicularbase=512
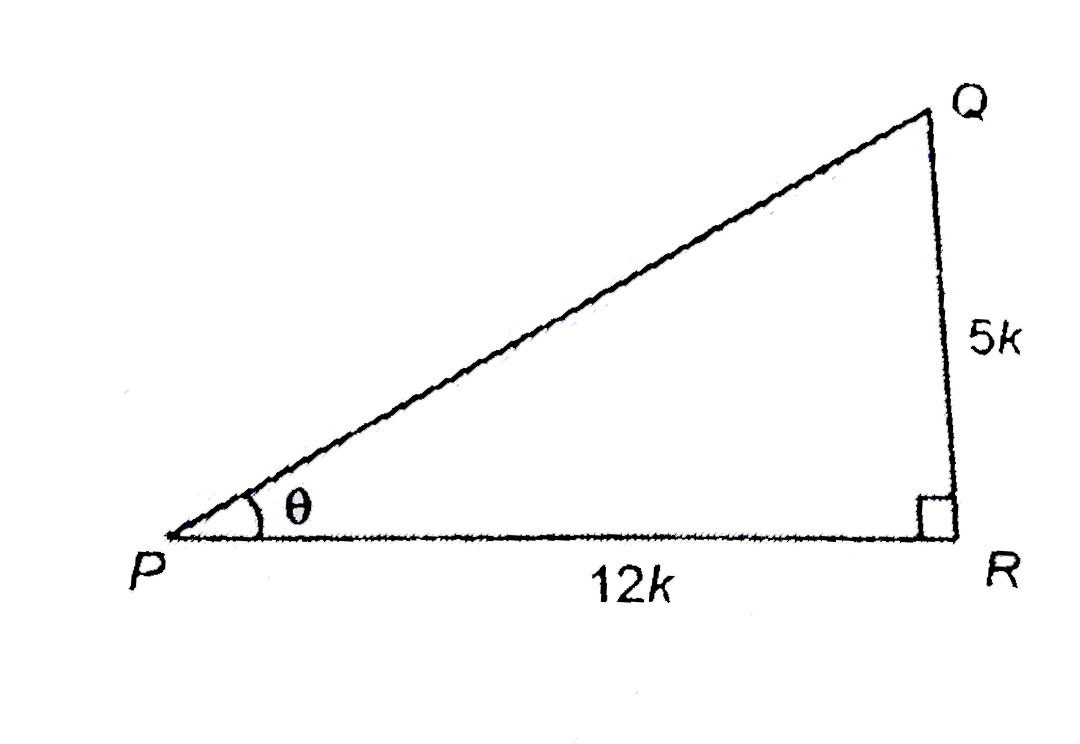
Now , constriuct a ΔPQR in which
PR=12k,QR=5kand∠QRP=90∘.
Let∠QPR=θ
In ΔPQR
From Pythagoras theorem
PQ2=PR2+QR2
⇒=(12k)2+(5k)2=144k2+25k2=16k2
⇒PQ=13k
Now ,
sinθ=perpendicularhypotenuse=QRPQ=5k13k=513
cosθ=basehypotenuse=PRPQ=12k13k=1213
cosecθ=hypotenuseperpendicular=PQQR=13k5k=135
secθ=hypotenusebase=PQPR=13k12k=1312
cotθ=baseperpendicular=PRQR=12k5k=125
|
Topper's Solved these Questions
- INTRODUCTION TO TRIGONOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Problems From NCERT/exemplar
29 Videos
- INTRODUCTION TO TRIGONOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Exercise 8a
20 Videos
- CONSTRUCTIONSBOOK - NAGEEN PRAKASHANCHAPTER - CONSTRUCTIONSEXERCISE - PROBLEMS FROM NCERT/ EXEMPLAR
10 Videos
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - NAGEEN PRAKASHANCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - Revision Exercise Long Answer Questions
8 Videos
Similar Questions
Given tanα=512 , find other trigonometric ratios
View SolutionIf Value of tanθ=815 , find other trigonometric ratios
View SolutionIf cosA=45 , find other trigonometric ratios.
View SolutionIf sinA=23 , find other trigonometric ratios.
View SolutionIf tanθ=11 , find other trigonometric ratios
View SolutionIf sinθ=1115 , find other trigonometric ratios
View SolutionIf cotθ=125 , find other trigonometric ratios
View SolutionGiven tanA=43, find the other trigonometric ratios of the angle A.
View SolutionIf cosθ=725 , find other trigonometric ratios
View Solutionsinθ=√32 , find other trigonometric ratios
View Solution
