Given that E= { Natural number up to 30 } P={xx=4y+1,x∈E}andQ={xx=6y+x∈E} Find n(P∩Q)
0
2
1
3
The correct Answer is:B
P = {5, 9, 13, 17, 21. 25, 29}
Q={7, 13, 19, 25}
P∩Q={13,25}
∴n(P∩Q)=2
Hence , the correct option is ( b)
Topper's Solved these Questions
- Set theoryBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - Set theoryEXERCISE - ASSESSMENT TEST Test 1
12 Videos
- Set theoryBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - Set theoryEXERCISE - ASSESSMENT TEST Test 2
12 Videos
- Set theoryBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - Set theoryEXERCISE - Concept Application Level 2
23 Videos
- RATIO AND ITS APPLICATIONSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - RATIO AND ITS APPLICATIONSEXERCISE - ASSESSMENT TESTS (TEST 2)
12 Videos
- SIMPLE INTEREST AND COMPOUND INTEREST BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - SIMPLE INTEREST AND COMPOUND INTEREST EXERCISE - Level 3
9 Videos
Similar Questions
A = { set of natural numbers }
B = { set of odd natural numbers}
then find (A∩B)
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
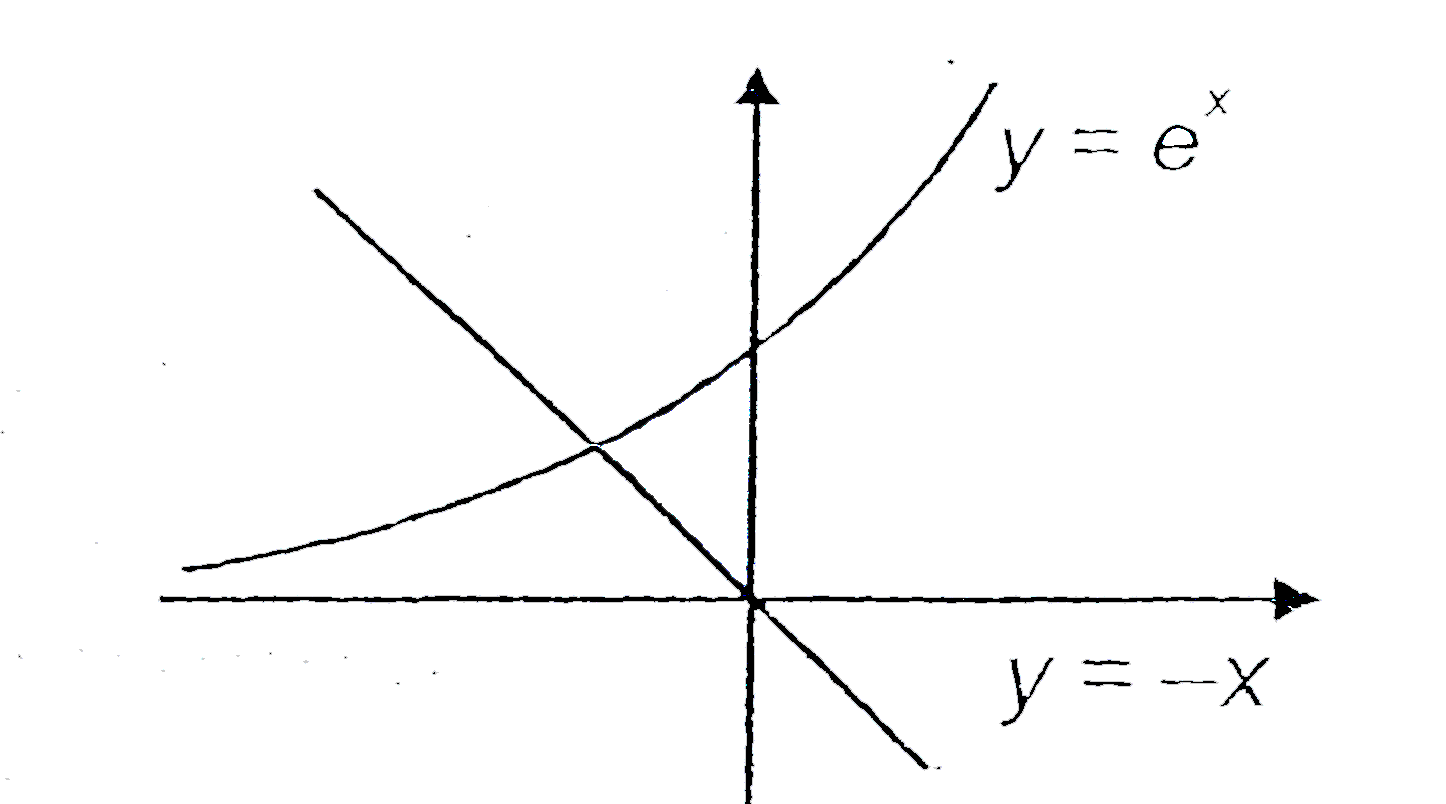
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A:{(x,y):y=√4−x2,x∈[−2,2]}
B={(x,y):y=|x|,x∈R}
Then n(A∩B)
View Solution
Knowledge Check
Given that E= { Natural number up to 30 } P={xx=4y+1,x∈E}andQ={xx=6y+x∈E} Find n(P∩Q)
A0B2C1D3E= { Natural numbers up to 30 }
X={xx=4y+2,y∈E}
Find n(X∩Y)A2B5C7D9P={x:x is a multiple of 4,x<20 } and Q= {xx is a multiple of 6,x<30} Find n(P) +n(Q).
The following steps are involved in solving the above problem .Arrange them in sequential order .(A) P= {4,8,12,16} and Q={6,12 , 18,24}
(B)⇒n(P) =4 and n(Q)=4
(C ) n(P) = 4 and n (Q) =8
ACBABACBCBACDABC
In some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
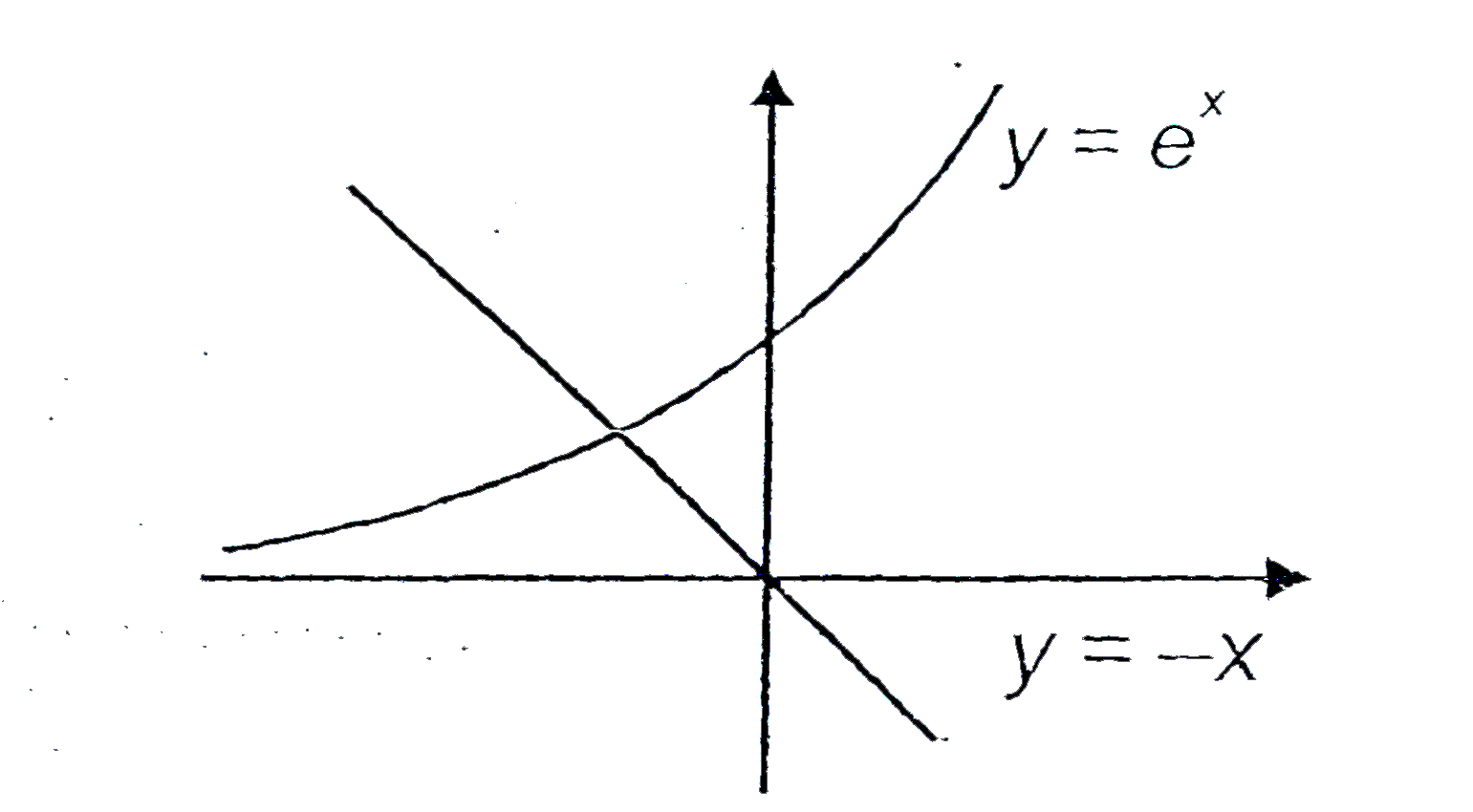
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):y=sinπx,x∈R}
B={(x,y):y=|In|x||,x∈R−{0}}
Then, n(A∩B)
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
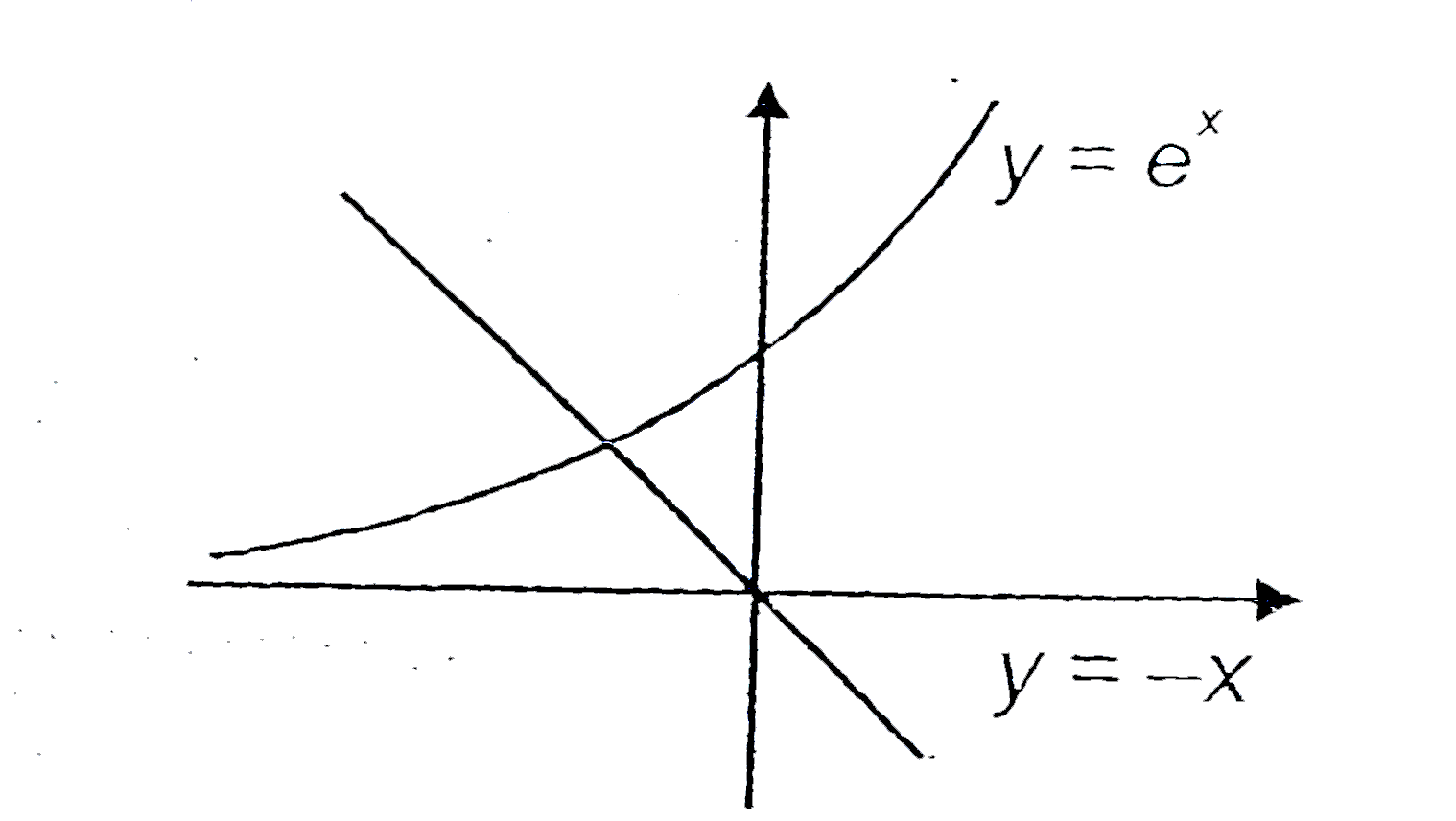
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):x2+y2≤2,x,y∈R}
B={{x,y):y≥x2,x,y∈R}
Then domain of A∩B is
View SolutionThe solution of the equation px+qy=m and qx+py=n is
View SolutionGiven X~ B (n,P)
If n= 10 and p=0.4 , find E(X) and Var (X) .
View SolutionGiven X ~ B ( n,p)If p =0 .6 E (X) =6, find n and Var (X)
View Solution
