In some question of sets, we have to make the use of graphs
For example
Find
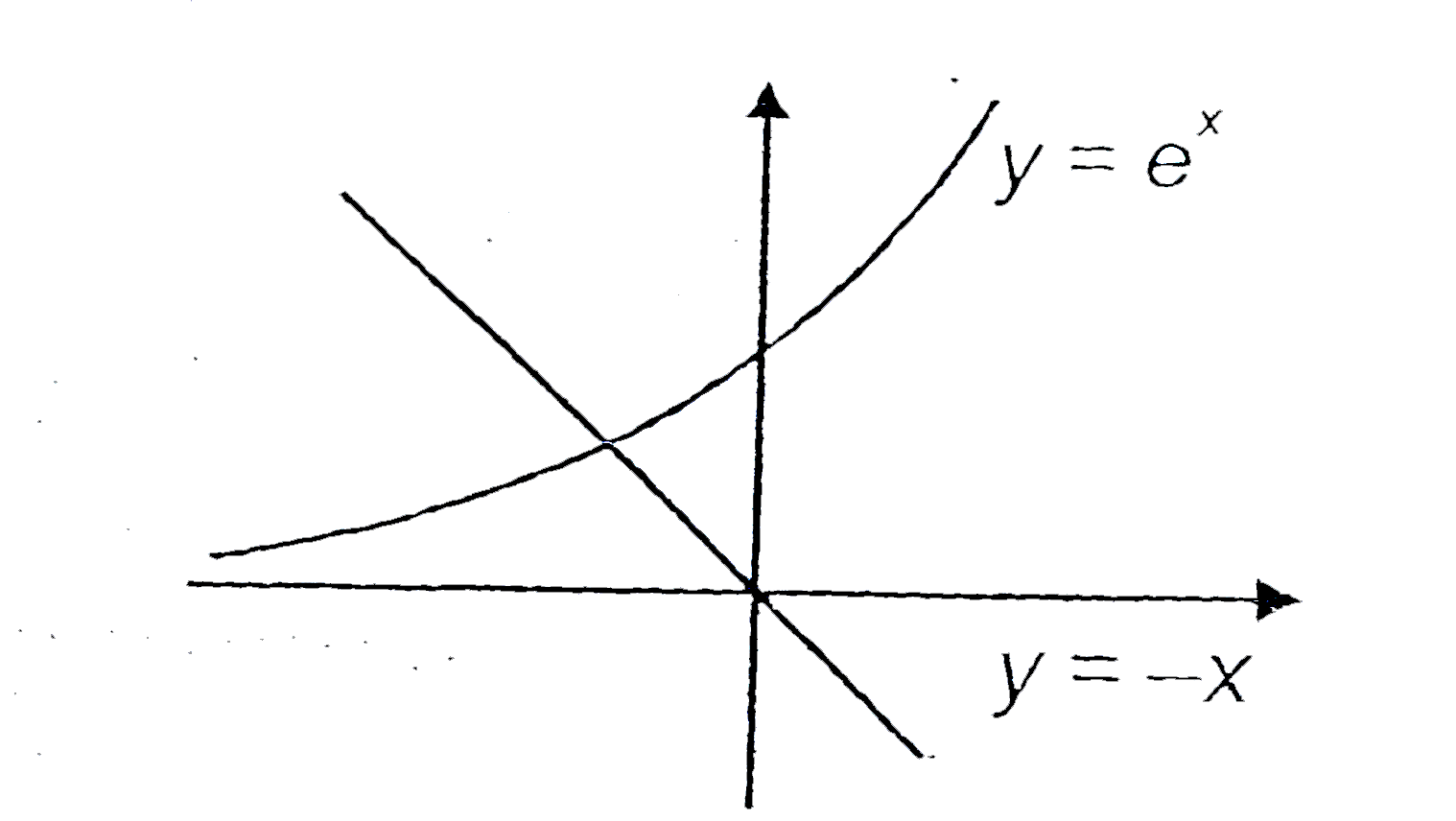
It is clear that intersect at one pont. Hence
Then domain of is
The correct Answer is:A
Step by step video & image solution for In some question of sets, we have to make the use of graphs For example A={(x,y):y=e^(x), x in R} B={{x,y}: y=-x. x in R} Find n(A cap B) It is clear that y=e^(x) and y=-x intersect at one pont. Hence n(A cap B)=1 A={(x,y):x^(2)+y^(2) le 2, x ,y in R} B={{x,y): y gex^(2),x,y in R} Then domain of A cap B is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SETS Book:AAKASH INSTITUTEChapter:SETS Exercise:COMPREHENSION-III
Explore 3 Videos
- SETS Book:AAKASH INSTITUTEChapter:SETS Exercise:SECTION-E(Assertion-Reason Type Questions)
Explore 2 Videos
- SETS Book:AAKASH INSTITUTEChapter:SETS Exercise:SECTION-D(Linked Comprehension Type Questions))
Explore 3 Videos
- SEQUENCES AND SERIES Book:AAKASH INSTITUTEChapter:SEQUENCES AND SERIES Exercise:Assignment (SECTION - J) Aakash Challengers
Explore 12 Videos
- STATISTICSBook:AAKASH INSTITUTEChapter:STATISTICSExercise:Section-C Assertion-Reason
Explore 15 Videos
Similar Questions
In some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
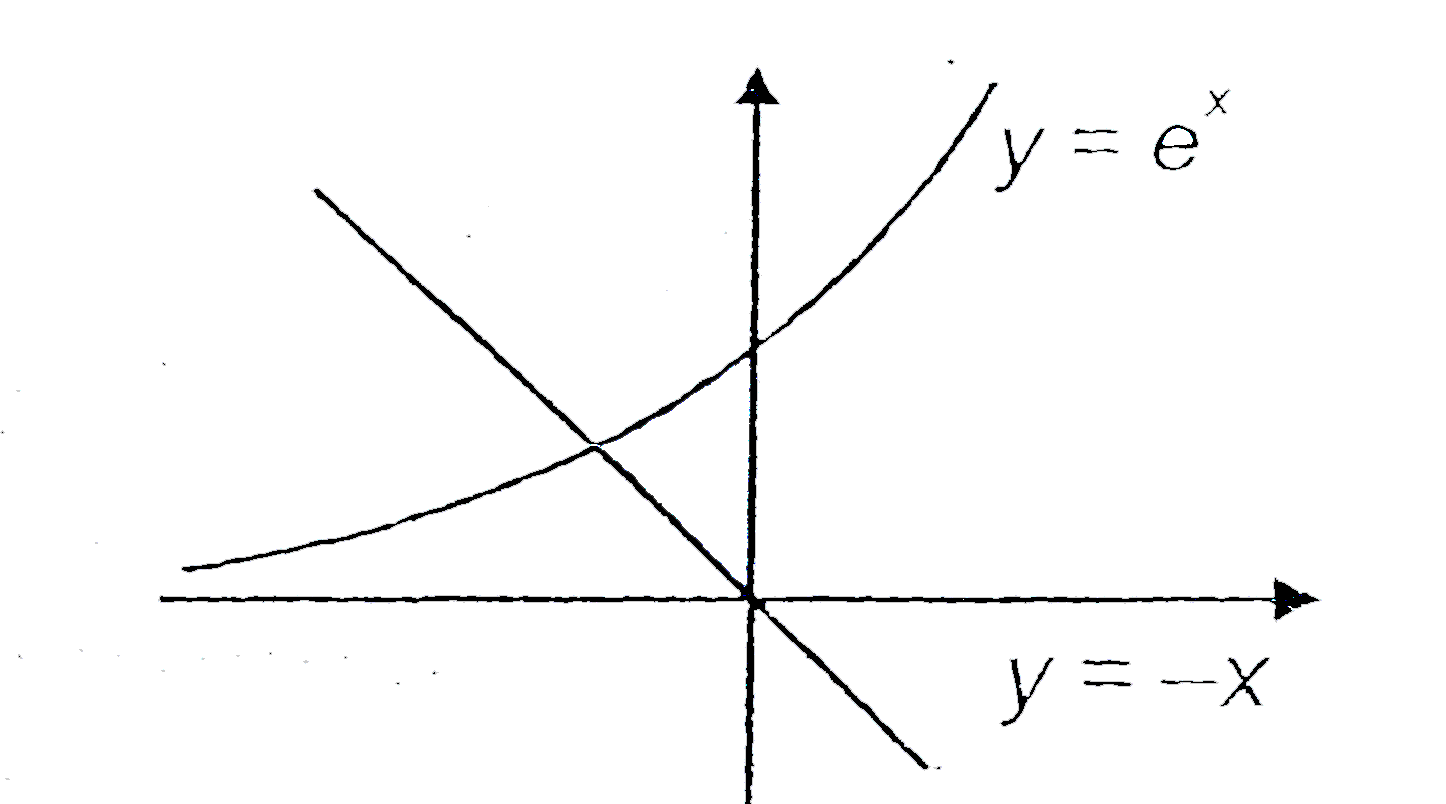
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A:{(x,y):y=√4−x2,x∈[−2,2]}
B={(x,y):y=|x|,x∈R}
Then n(A∩B)
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
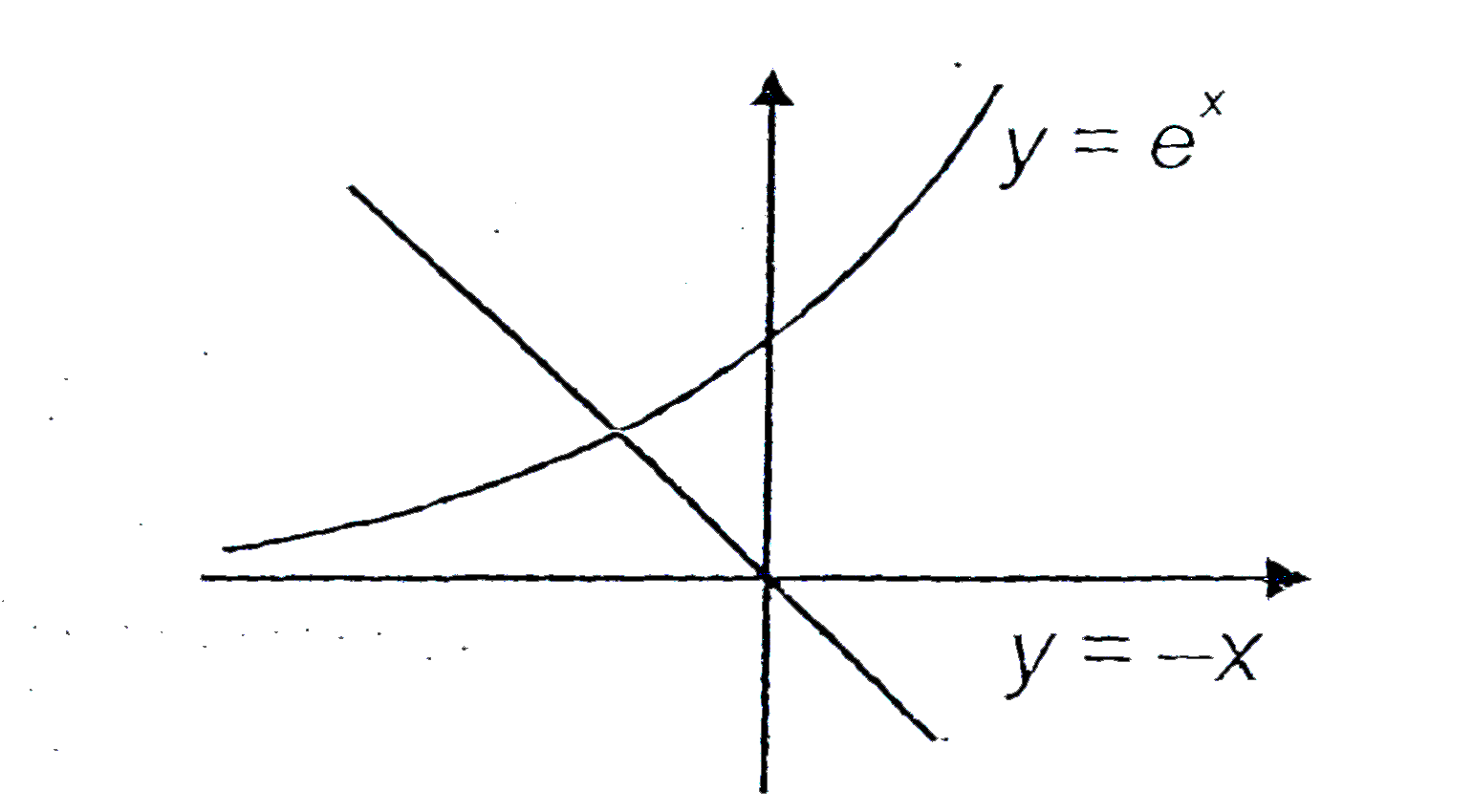
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):y=sinπx,x∈R}
B={(x,y):y=|In|x||,x∈R−{0}}
Then, n(A∩B)
View Solution
Knowledge Check
Let A={(x,y):y=ex,x∈R}B={(x,y),Y=e−x,x∈R}then
AA∩B=ϕBA∩B≠ϕCA∪B=R2Dnone of theseLet A={(x,y):y=ex,x∈R}B={(x,y),Y=e−x,x∈R}then
AA∩B=ϕBA∩B={(0,1)}CA∪B=R2DA∩B={(0,0)}ifA={(x,y):x2+y2=4,x,y∈R}and
B={(x,y):x2+y2=9,x,y∈R},thenAA−B=ϕBB−A=BCA∩B≠ϕDA∩B=A
If A={(x,y):y=ex,x∈R} and B={(x,y):y=e−2x,x∈R}, then
View SolutionLet A={(x,y)∣y=ex,x∈R}andB={(x,y)∣=e−x,x∈R}. Then
View SolutionifA={(x,y):x2+y2=4,x,y∈R}and
B={(x,y):Y=|x|,x,y∈R} then
View SolutionIf A={(x,y):x2+y2≤1:x,y∈R} and B={(x,y):x2+y2≥4,x,y∈R}, then
View SolutionIf A={(x,y):x2+y2≤1:x,y∈R} and B={(x,y):x2+y2≥4,x,y∈R}, then
View Solution