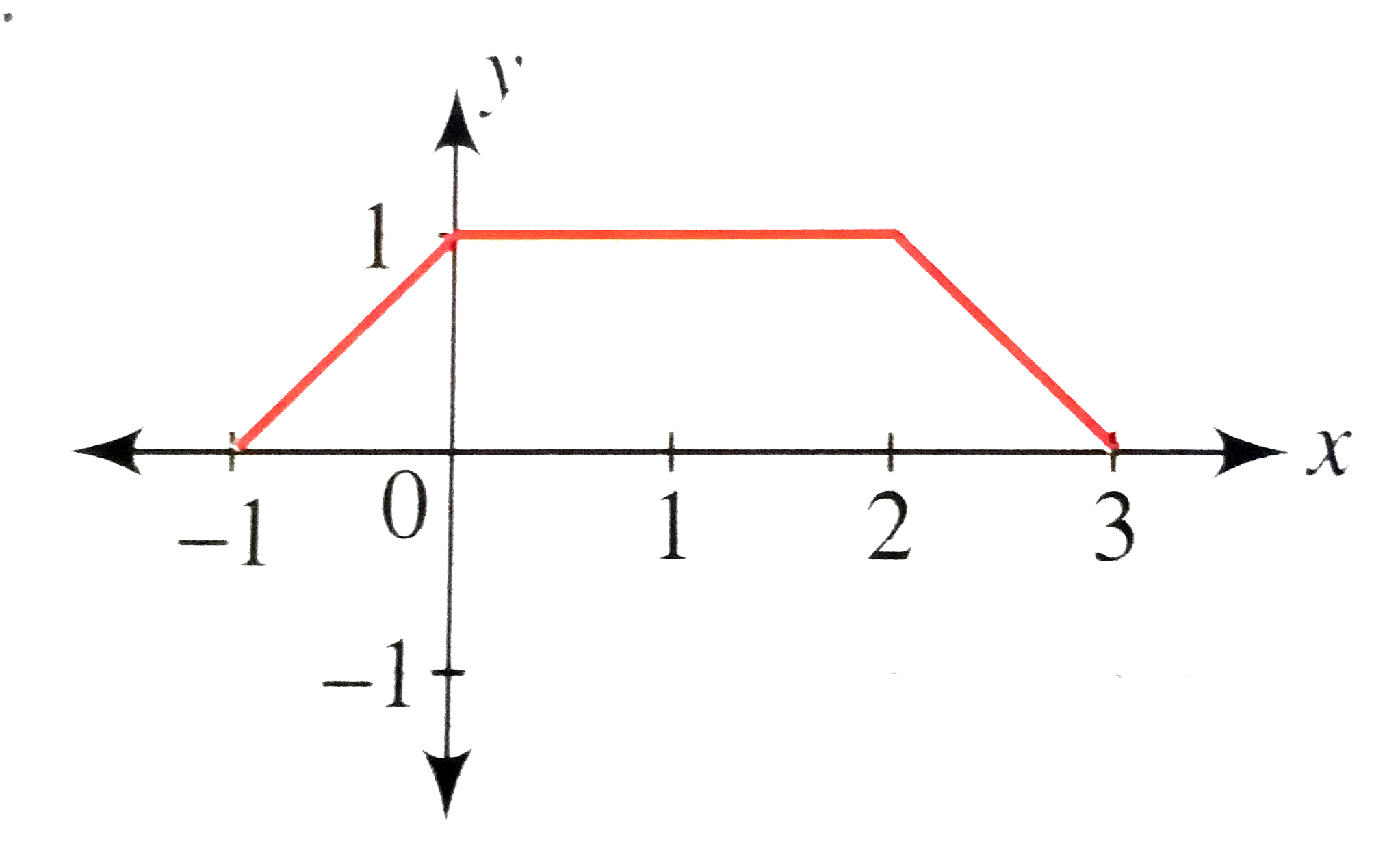
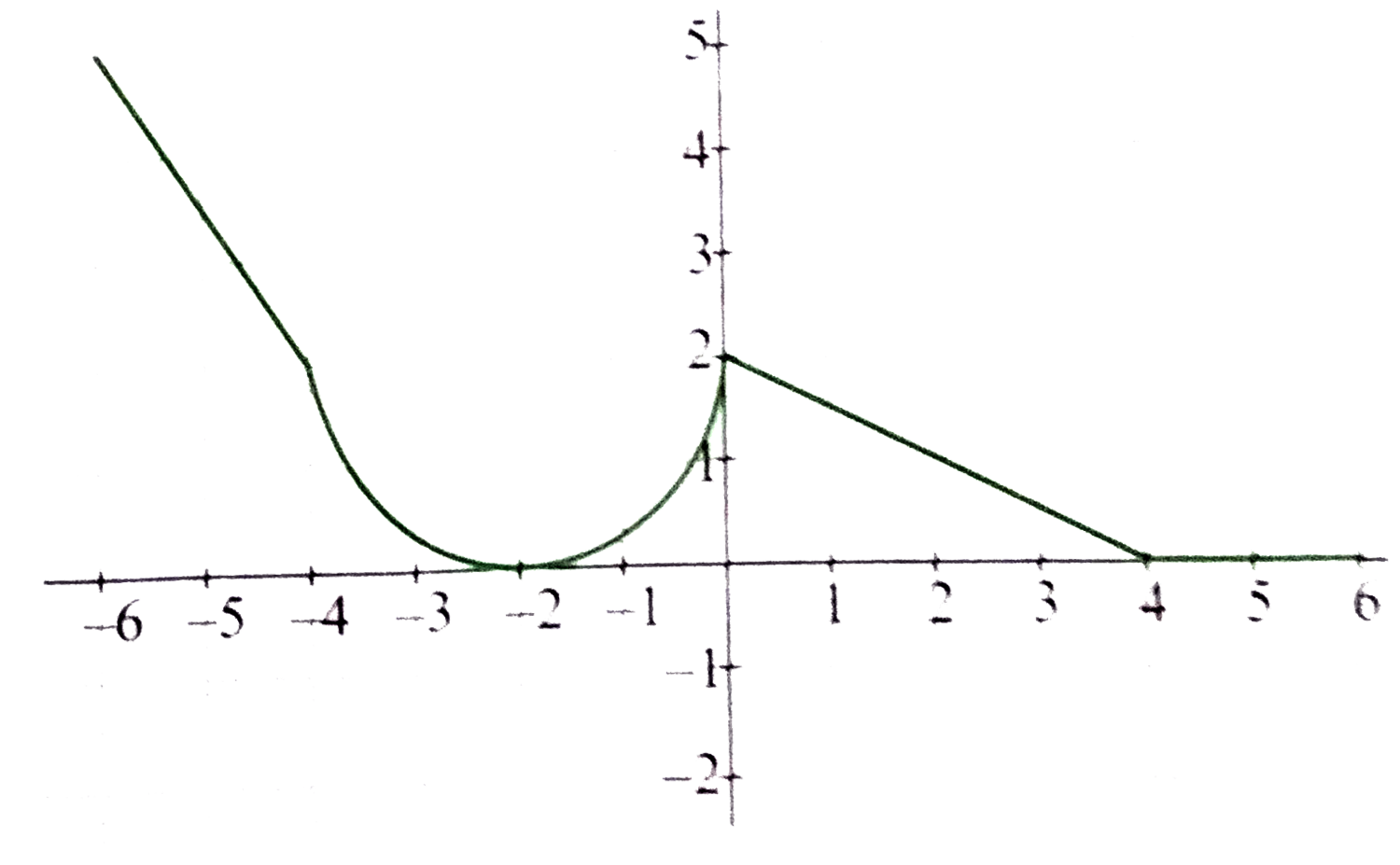
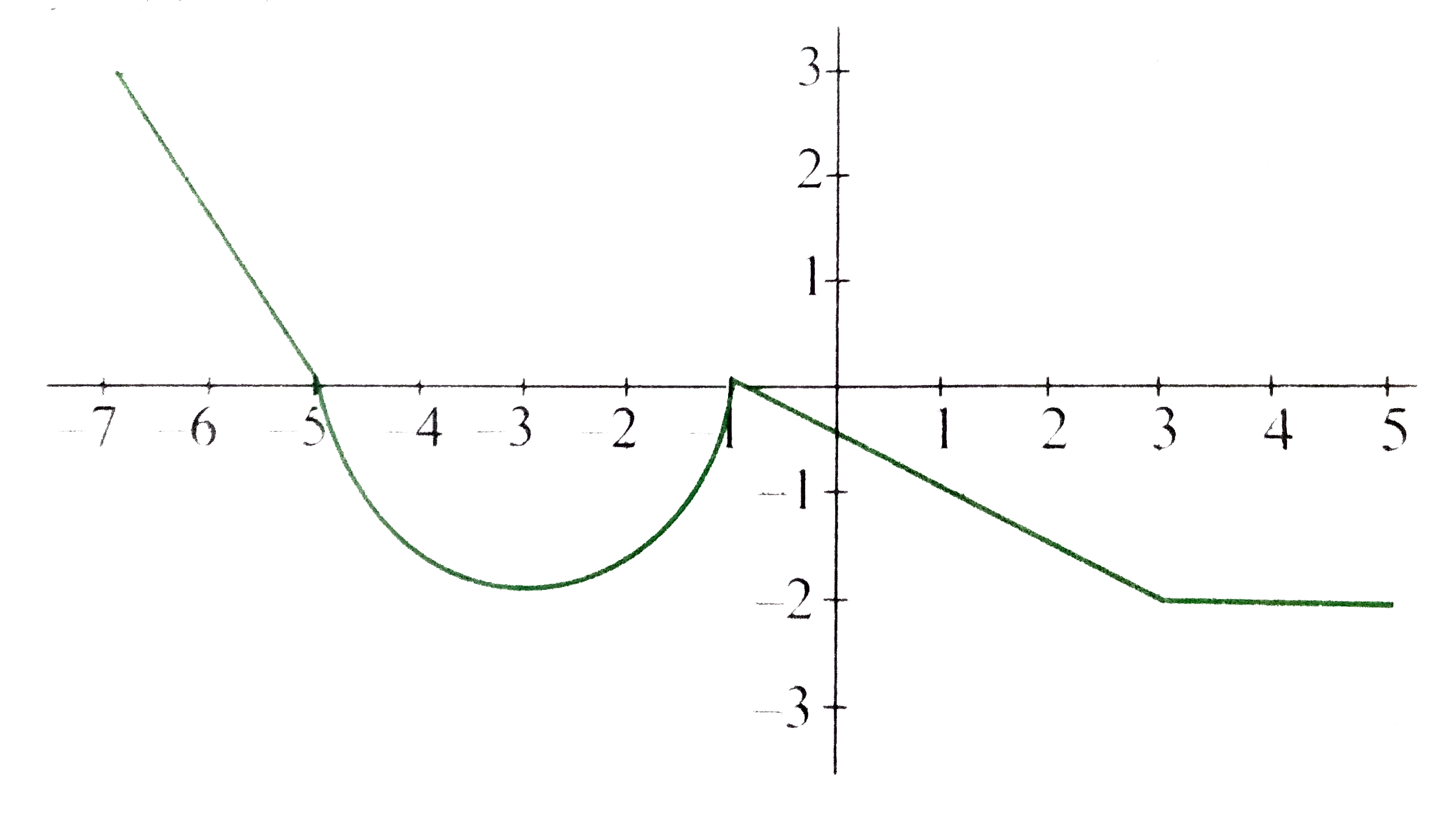
Given the graph of f(x), draw the graph each one of the following functions :
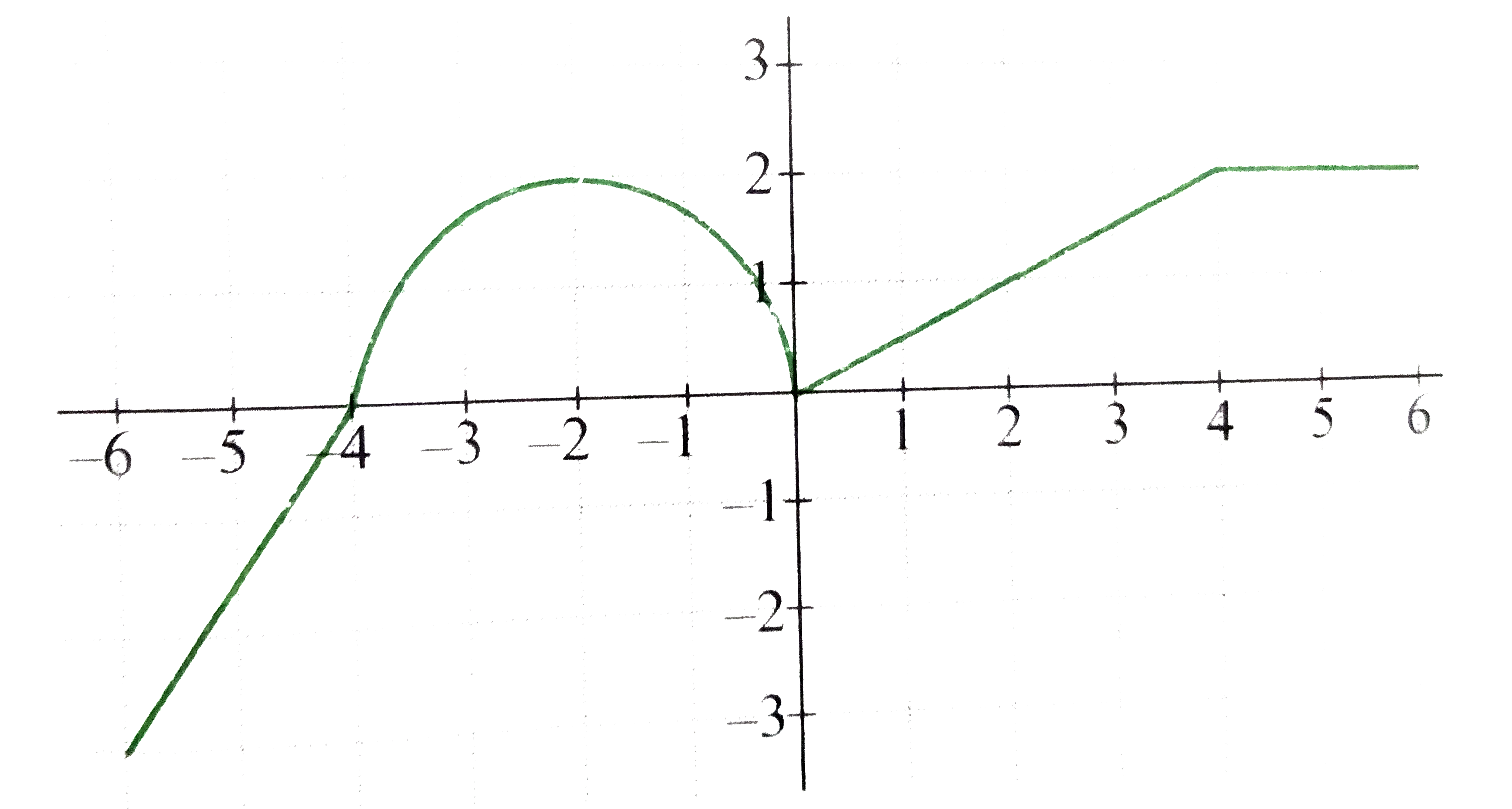
(a) y=f(x)+3 (b) y=−f(x)+2
(c ) y=f(x+1)−2 (d) y=−f(x−1)
(e ) y=f(−x) (f) y=f(|x|)
(g) y=f(1−x)
Text Solution
(a) For y=f(x)+3, shift the graph of y=f(x),3 units upward.
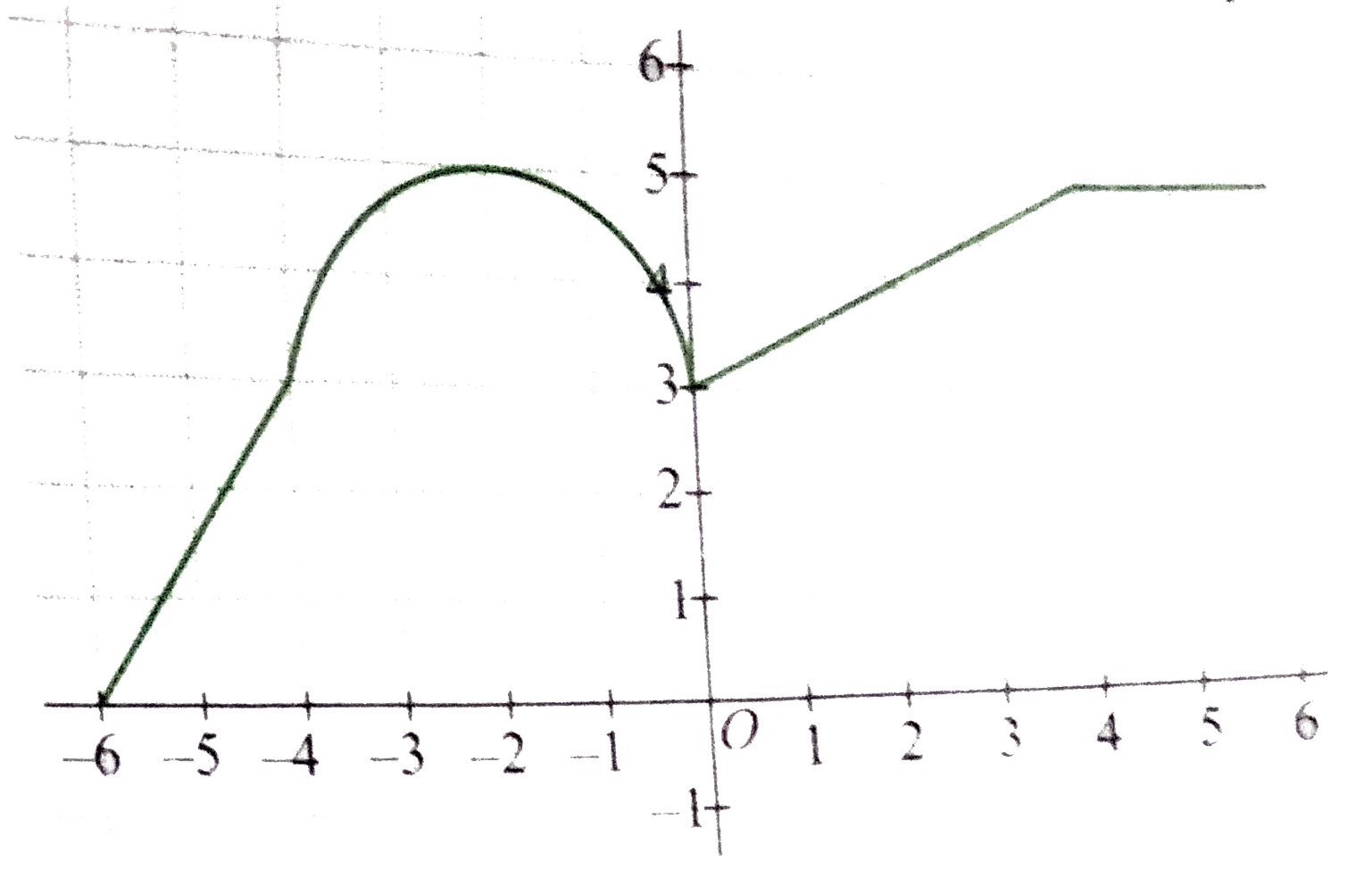
(b) y=−f(x)+2
First graph of y=f(x) about x-axis to get y=−f(x).
Now, shift the above graph 2 units upward to get y=2−f(x).
(c ) y=f(x+1)−2
First shift the graph of y=f(x), 1 units left to get y=f(x+1).
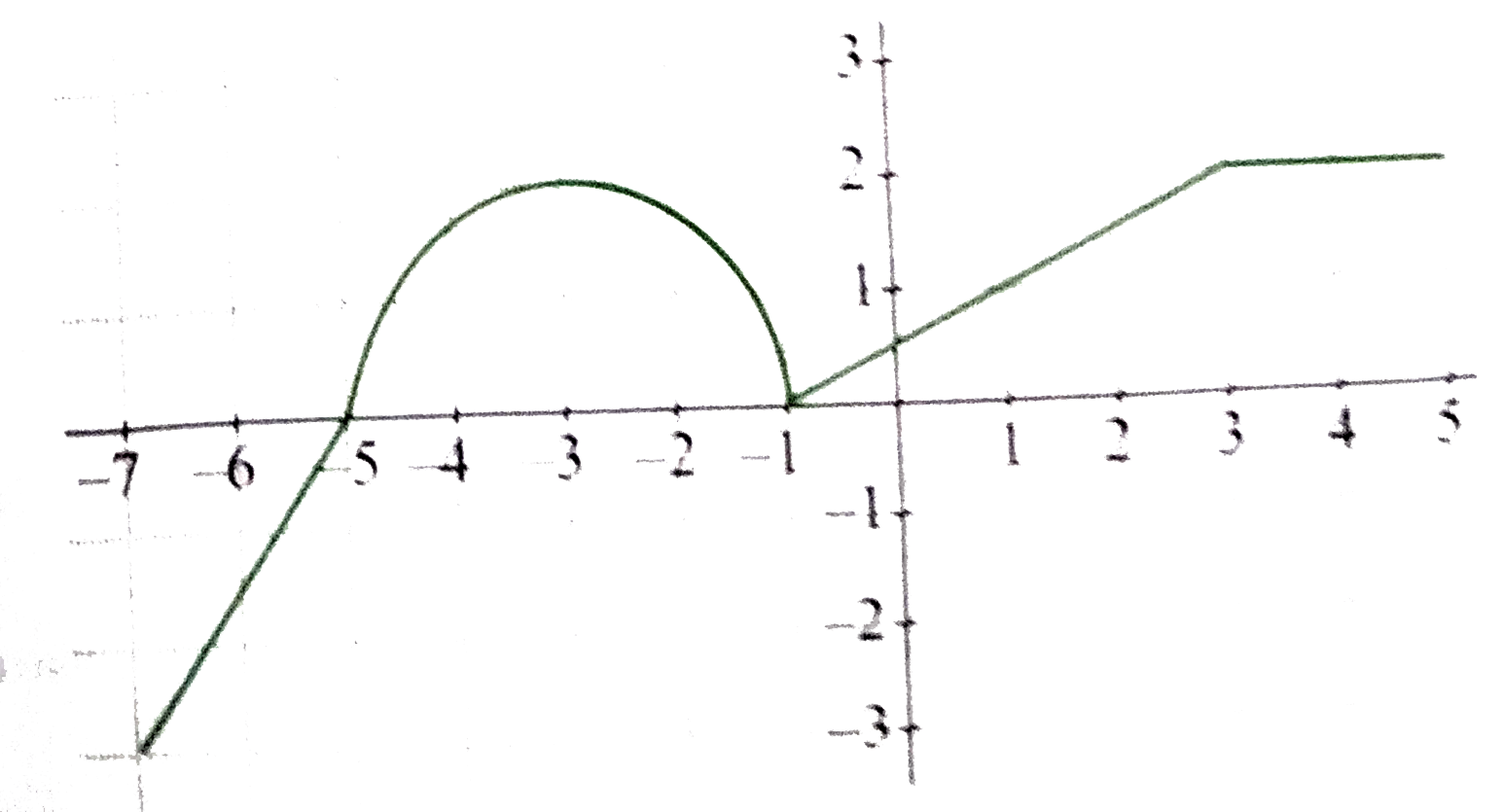
Now shift the above graph 2 units downward to get
y=f(x+1)−2.
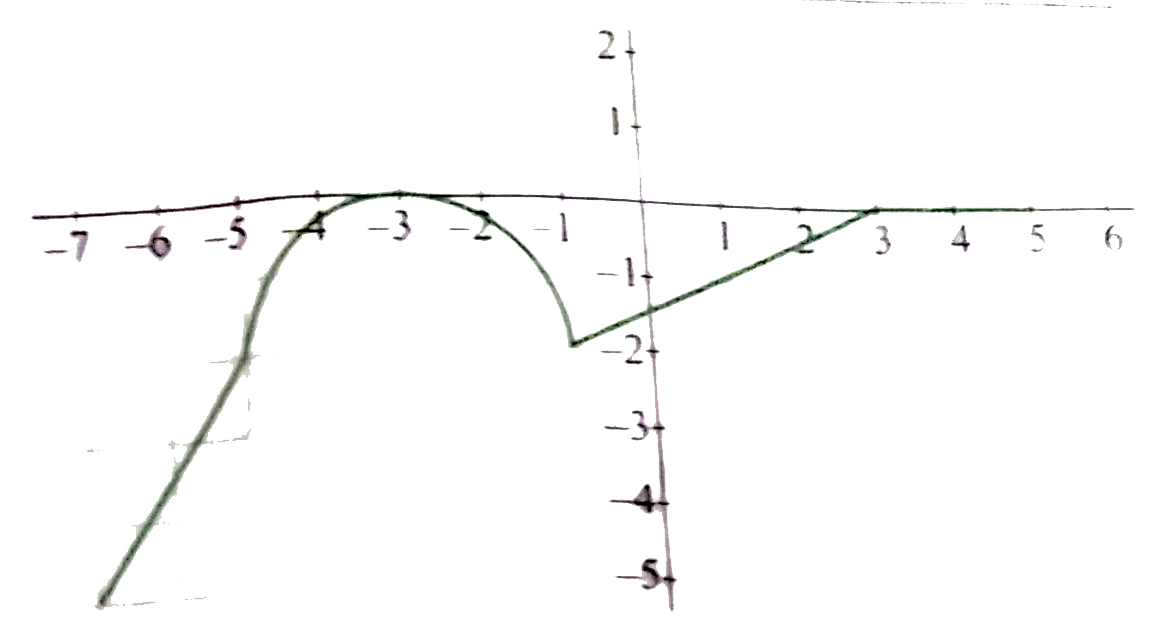
(d) y=−f(x−1)
First shift the graph of y=f(x), 1 unit right to get y=f(x−1).
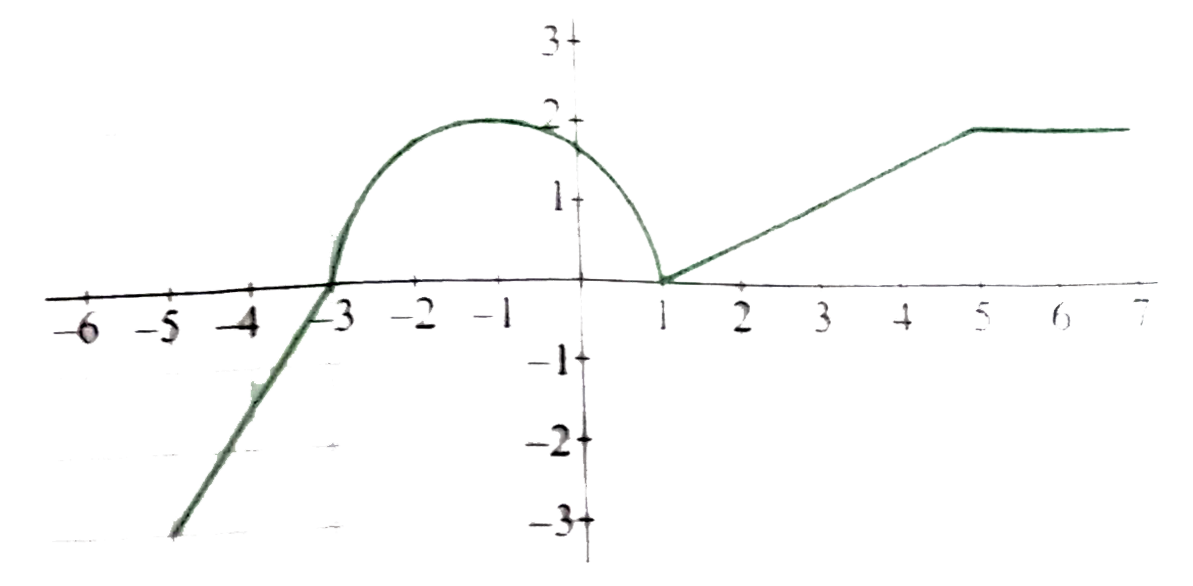
Now, flip the above graph about x- axis to get y=−f(x−1).
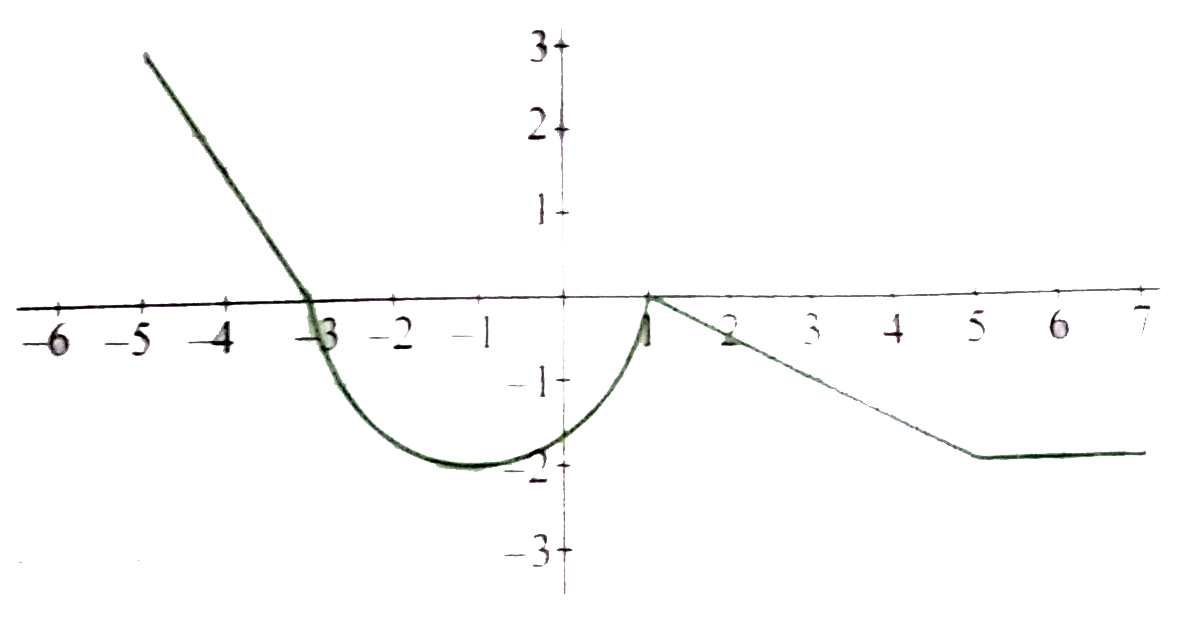
(e ) y=f(−x)
Flip the graph about y-axis to get y=f(−x).
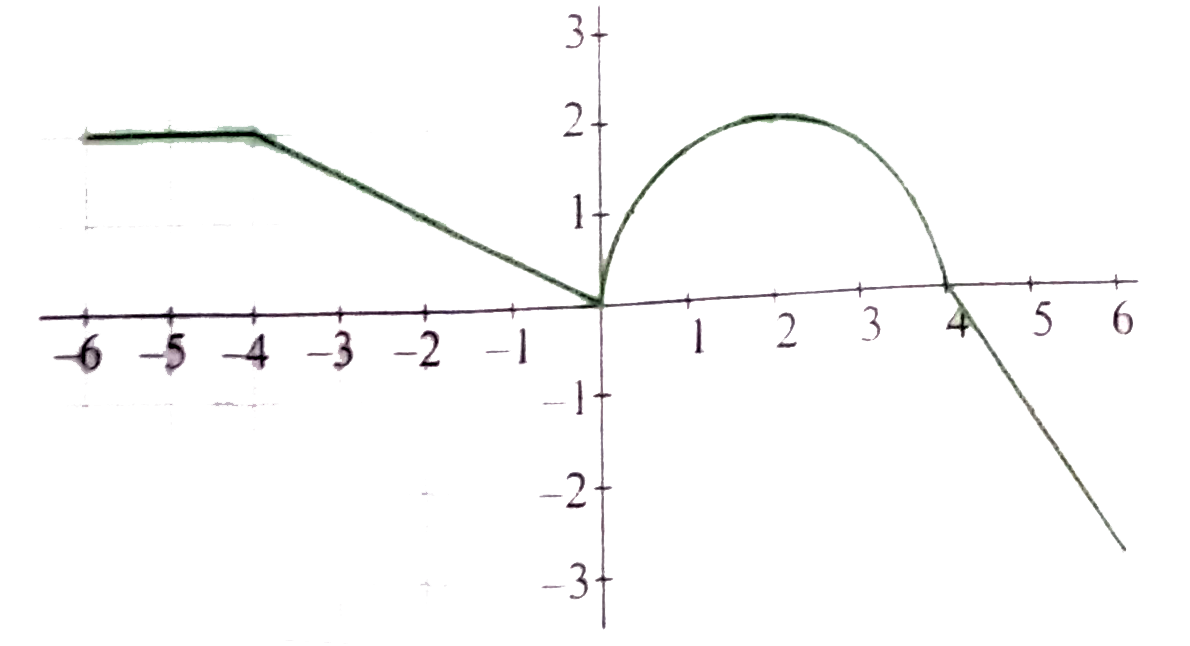
(f) y=f(|x|)
Neglect the graph of y=f(x) for x<0 and take the mirror image of y=f(x) for x>0 about y-axis, keeping y=f(x) for x>0.
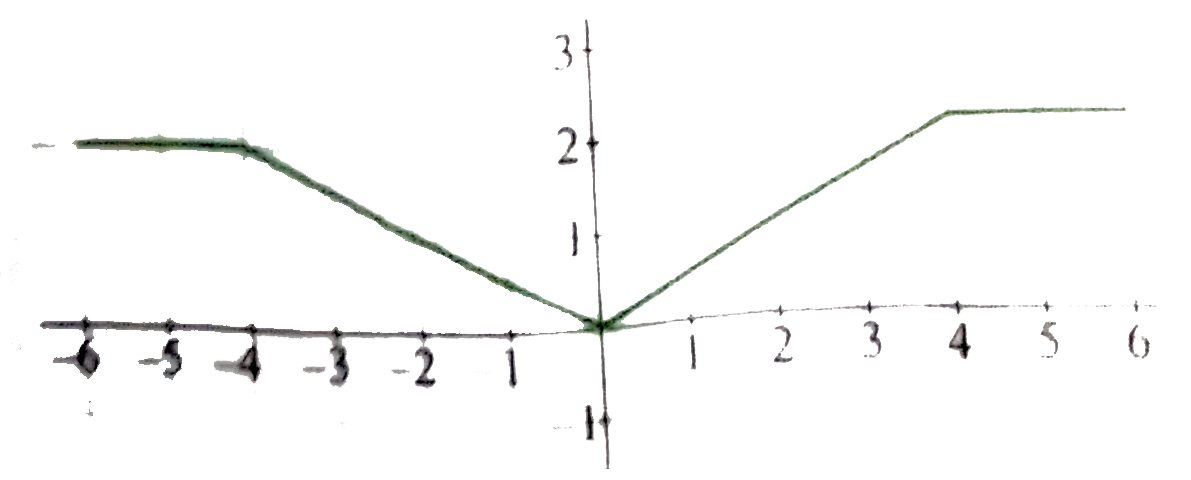
(g) y=f(1−x)
First flip the graph to get y=f(−x) as in (e ). Then shift y=f(−x), 1 unit left hand side to get y=(1−x).
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the graph of the function y=f(x) is as shown :

The graph of y=1/2(|f(x)|−f(x)) isA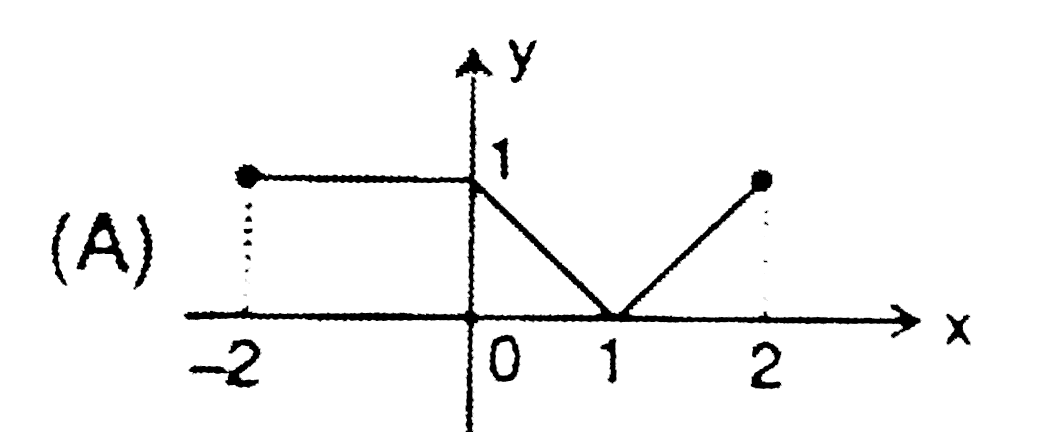 B
B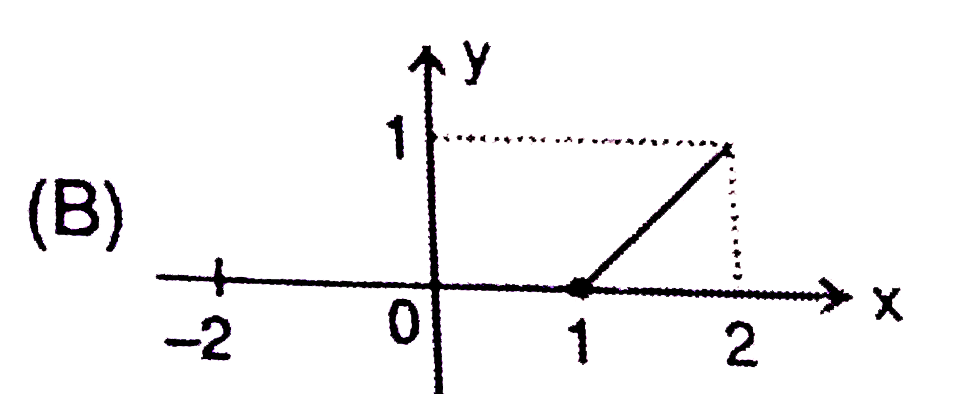 C
C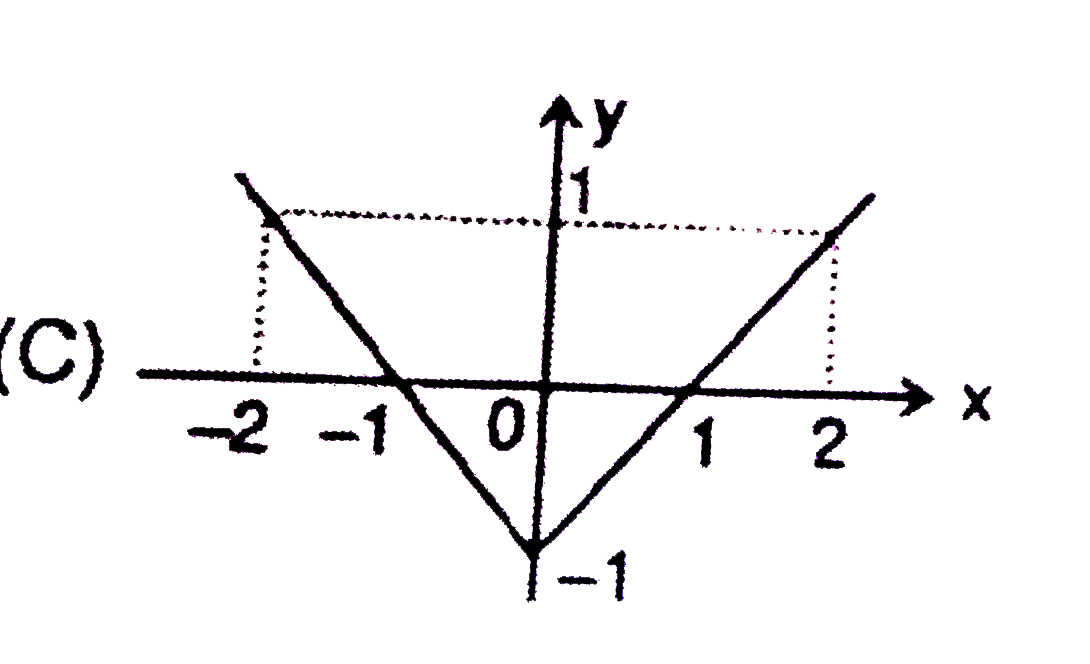 D
D
If f(x)=sin(πx), then draw the graph of the followings : (i) y=f(|x|) (ii) y=f(−|x|) (iii) |y|=f(x)
View SolutionConsider the function f(x)={2x+3,x≤1and−x2+6,x>1 Then draw the graph of the function y=f(x),y=f(|x|),y=|f(x)|,andy=|f(x)|.
View SolutionIf the graph of the function y=f(x) is as shown :

The graph of y=1/2(|f(x)|−f(x)) is
View SolutionIf the graph of the function y=f(x) is as shown :

the graph of y=12(|f(x)|−f(x)) is
View SolutionIf the graph of the function y=f(x) is as shown :

The graph of y=1/2(|f(x)|−f(x)) is
View SolutionIf the graph of the function y=f(x) is as shown : the graph of y=12(|f(x)|−f(x)) is
View SolutionThe graph y = f (x) is as shown:
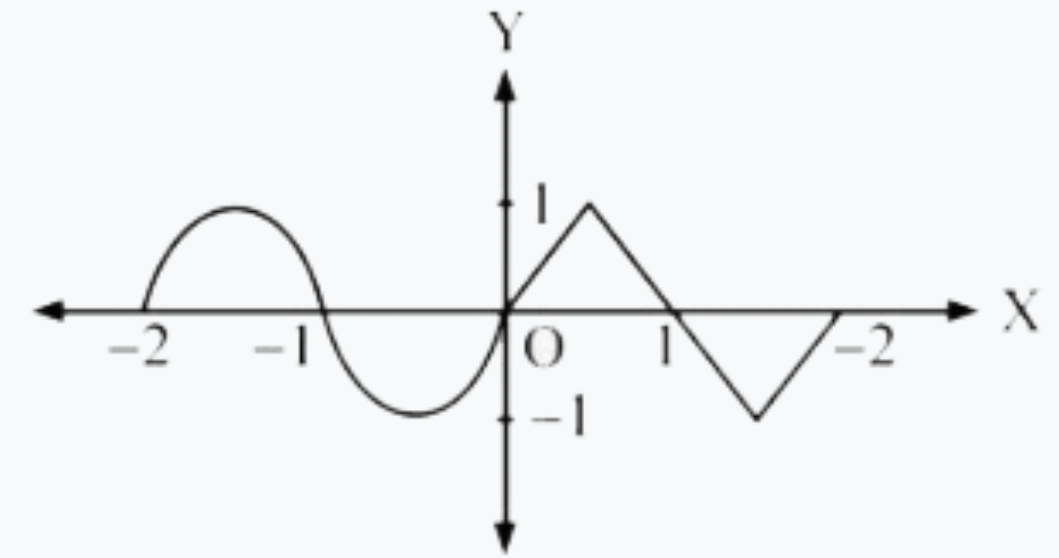
The graph of y = f (–|x|) is:
View Solution