(i)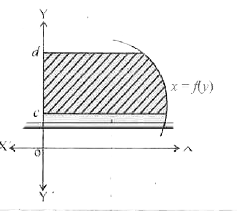
Area of the shaded portion in the figure is equal to
(a) ∫cdf(x)dx (b) ∫dcf(x)dx
(c)∫cdf(y)dy (d) ∫dcf(y)dy
(ii) Consider the curve y=x2,x=0,y=1,y=4.Draw a rough sketch and shade the region bounded by the these curves. Find the area of the shaded region.Solution in Tamil
The correct Answer is:(i)d. ∫dcf(y)dy
ii.283sq.units
Step by step video, text & image solution for (i) Area of the shaded portion in the figure is equal to (a) int_(d)^(c)f(x)dx (b) int_(c)^(d) f(x) dx (c)int_(d)^(c)f(y)dy (d) int_(c)^(d)f(y)dy (ii) Consider the curve y = x^(2), x = 0, y = 1, y = 4.Draw a rough sketch and shade the region bounded by the these curves. Find the area of the shaded region. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - APPLICATION OF INTEGRALSEXERCISE - NCERT TEXT BOOK EXERCISE 8.113videos
APPLICATION OF INTEGRALS
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - APPLICATION OF INTEGRALSEXERCISE - NCERT TEXT BOOK EXERCISE 8.27videos
APPLICATION OF INTEGRALS
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - QUESTIONS FROM COMPETITIVE EXAMS51videos
BINOMIAL THEOREM
Similar Questions
Find the area of the region bounded by the curve y2=x and the lines x = 1, x = 4 and the x -axis.
05:41View SolutionFind the area of the circle4x2+4y2=9 which is interior of the parabola x2=4y.
01:47View SolutionIf T, denotes the rth term in the expansion of [x+1x]23, then
01:25View SolutionWhich of the following is incorrect? ∫b+ca+cf(x)dx=∫baf(x+c)dx ∫bcacf(x)dx=c∫baf(cx)dx ∫a−af(x)dx=12∫a−a(f(x)+f(−x)dx None of these
02:28View SolutionP(alpha,f(alpha)) and Q(beta,f(beta)) are ends of an arc in the first quadrant.The area bounded by the arc,ordinates through P and Q, and the x -axis is (A) int_(f(alpha))^(f(beta))f^(-1)(y)dy(B)int_(alpha)^( beta)f^(-1)(y)dy(C)int_(alpha)^( beta)f(x)dx(D)int_(f(alpha))^(f(beta))f(x)dx
01:21View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
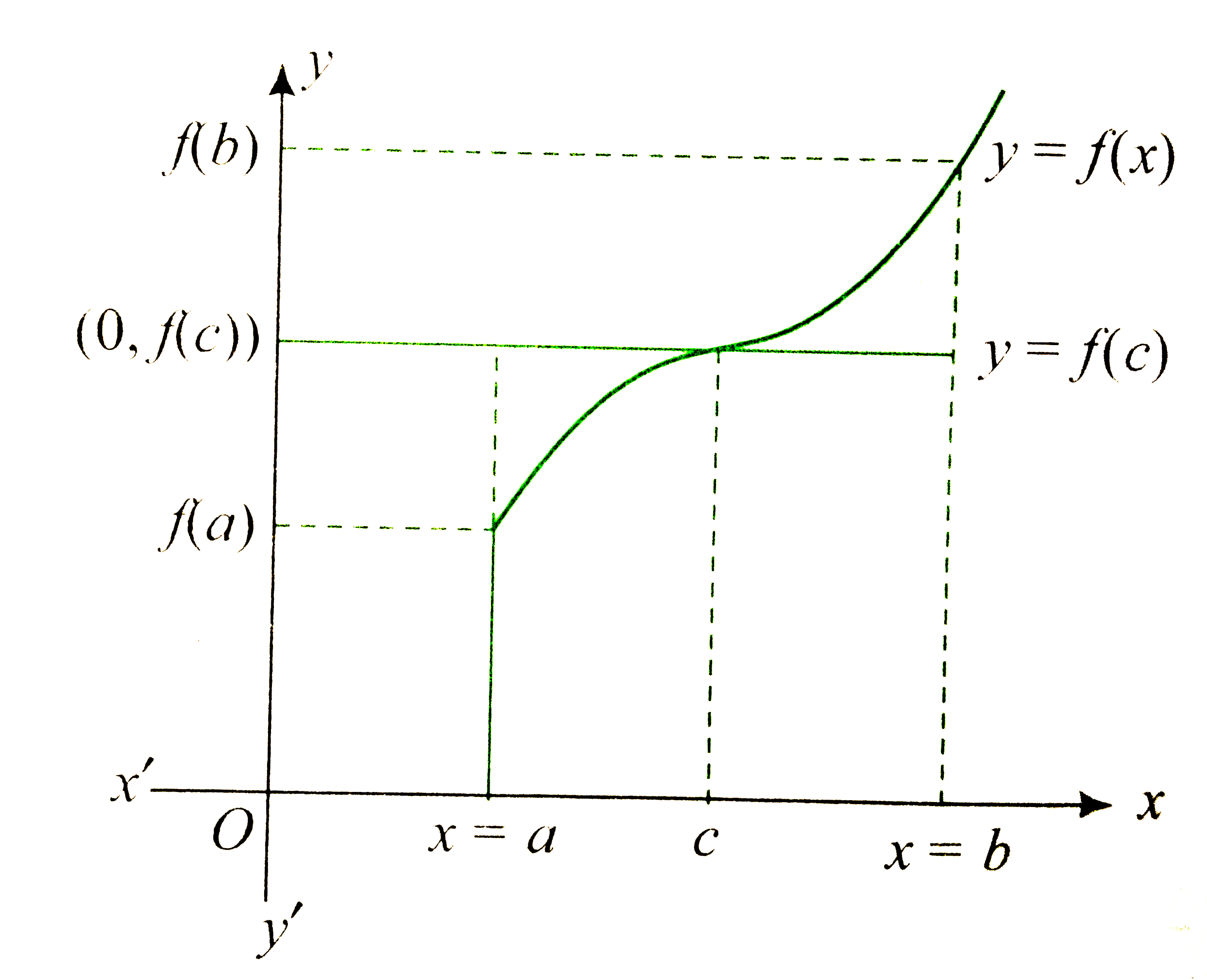
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
The value of the parameter a for which the area of the figure bounded by the abscissa axis, the graph of the function y=x3+3x2+x+a, and the straight lines, which are parallel to the axis of ordinates and cut the abscissa axis at the point of extremum of the function, which is the least, is02:11View Solution∫badx=∫caf(x)dx+∫caf(x)dx,a<c<b.
View SolutionIf ∫10f(x)dx=1 and ∫21f(y)dy=2, then ∫20f(z)dz=
01:16View SolutionIf ∫30f(x)dx=1 and ∫40f(y)dy=2, then ∫43f(z)dz=
02:27View SolutionIf ∫b−c0f(x+c)dx=a∫cbf(x)dx, then a =
02:00View SolutionIf X= {a,b,c,d} , Y = {f , b,d,g} , find:
(i) X-Y
(ii) Y-X.07:10View Solution(i) Draw a rough sketch of the curve y2=x and shade the region bounded by the line x = 1 and the curve.
(ii) Using integration find the area of the shaded region.03:21View SolutionIf ∫b−c0f(x+c)dx=k∫cbf(x)dx then k=
04:05View SolutionMatch the following
List - 1List - III) ∫1−1x|x|dxa) π2II) ∫π20(1+log(4+3sinx4+3cosx))dxb) ∫π20f(x)dxIII) ∫a0f(x)dxc) ∫a0[f(x)+f(−x)]dxIV) ∫a−af(x)dxd) 0e) ∫a0f(a−x)dx03:54View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b))isminiμmwhen
c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx

Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
The value of the parameter a for which the area of the figure bounded by the abscissa axis, the graph of the function y=x3+3x2+x+a, and the straight lines, which are parallel to the axis of ordinates and cut the abscissa axis at the point of extremum of the function, which is the least, is04:17View Solution

