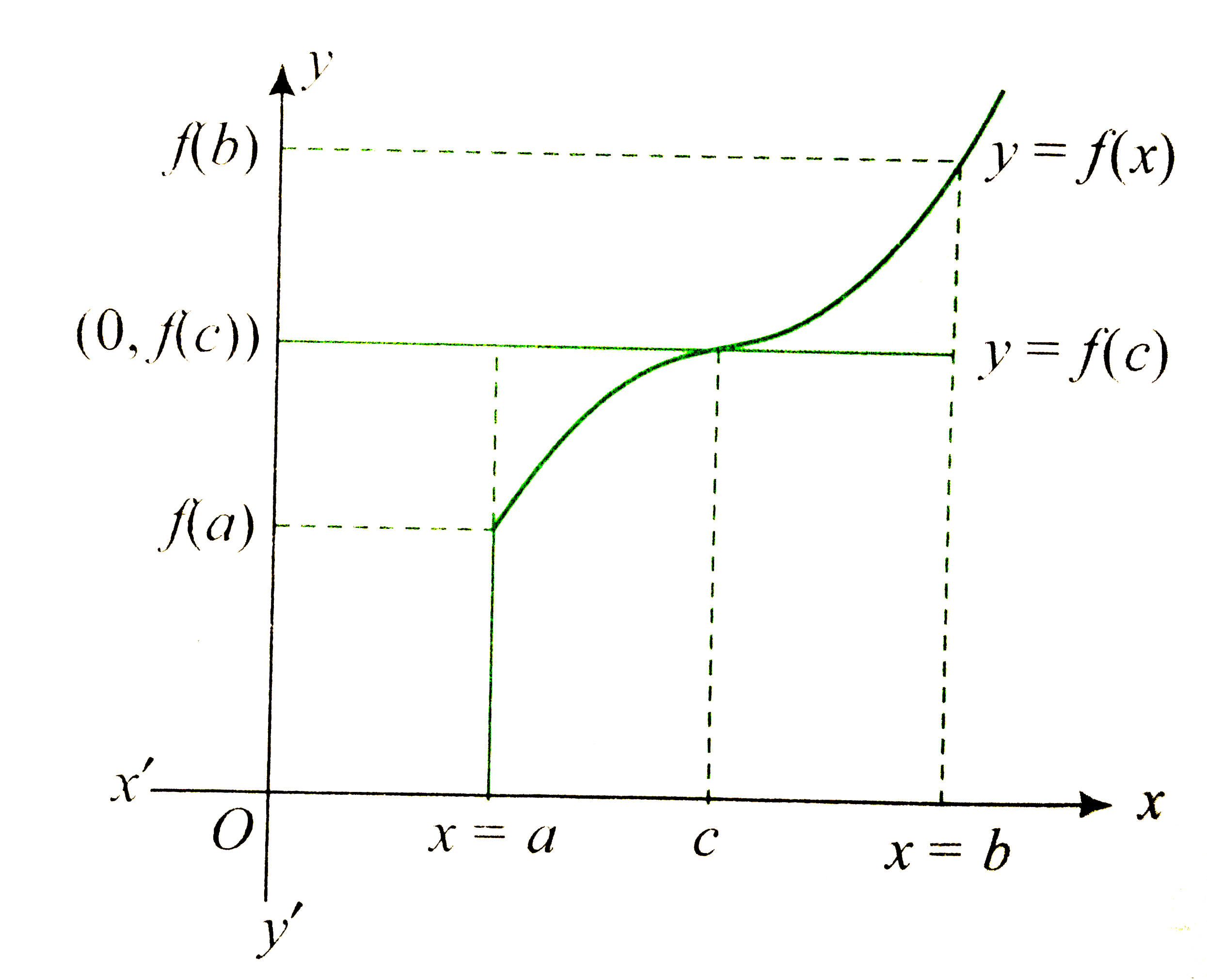
If y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b))isminiμmwhen
c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
The value of the parameter a for which the area of the figure bounded by the abscissa axis, the graph of the function y=x3+3x2+x+a, and the straight lines, which are parallel to the axis of ordinates and cut the abscissa axis at the point of extremum of the function, which is the least, is
2
0
-1
1
The correct Answer is:C
f(x)=x3+3x2+x+a
f'(x)=3x2+6x+1=0
⇒ x=−1±√63.
Hence, f(x) cuts the x-axis at
12[(−1+√63)+(−1−√63)]=−1.
f(−1)=−1+3−1+a=0
a=−1.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Matrix Match Type5videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Numerical Value Type18videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Multiple Correct Answers Type13videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type5videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix4videos
BINOMIAL THEOREM
Similar Questions
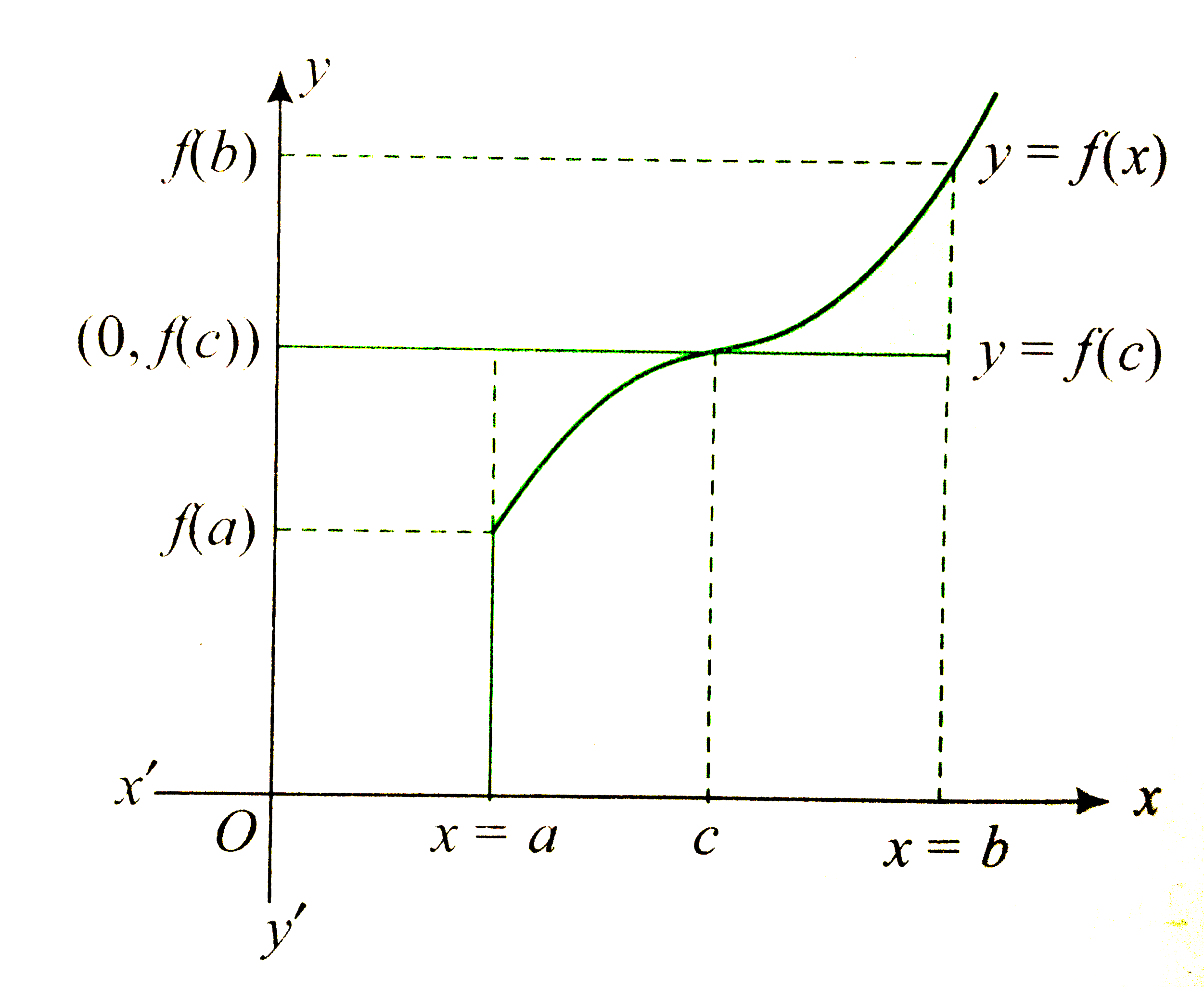
If y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
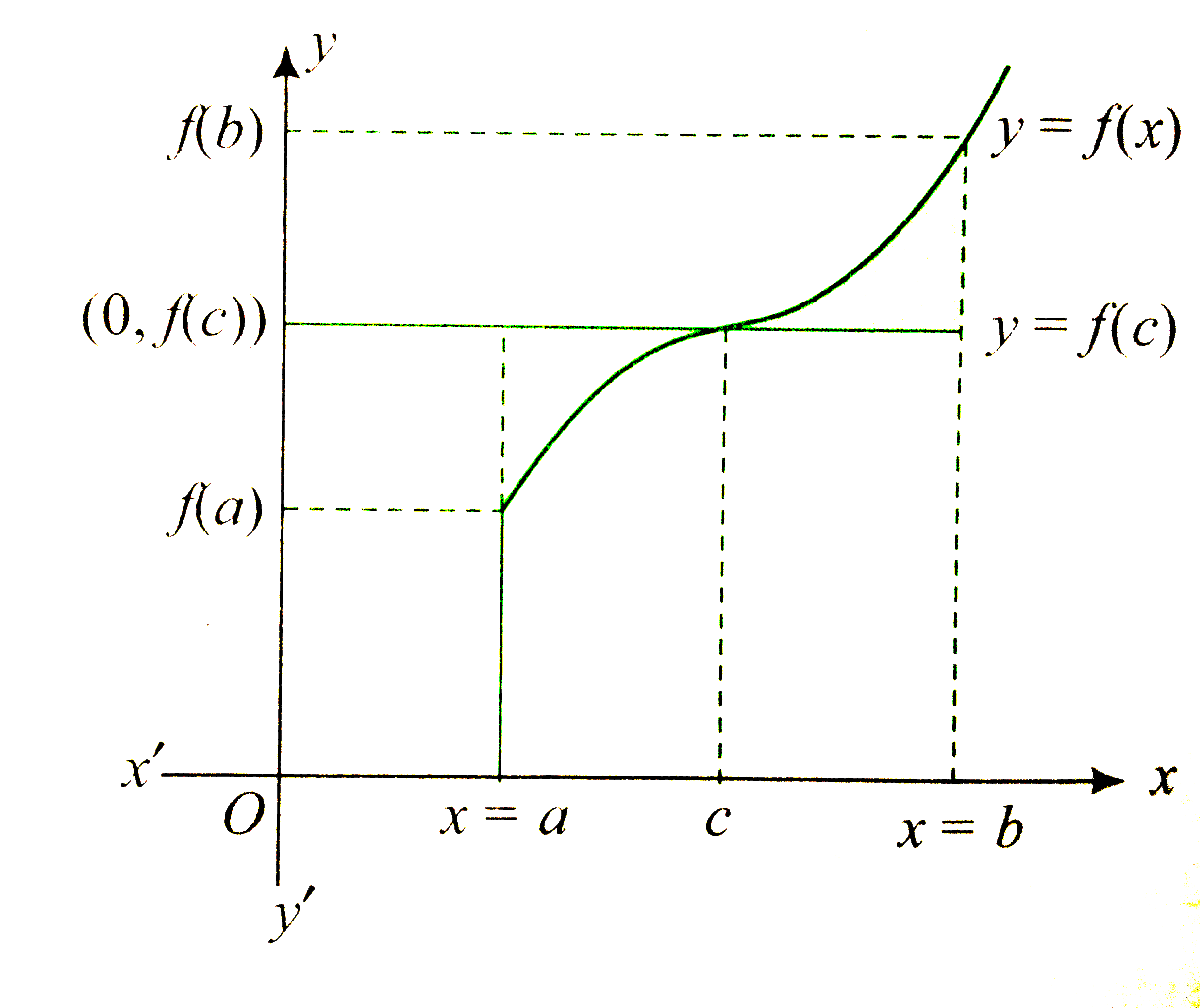
If the area enclosed by f(x)=sinx+cosx,y=a between two consecutive points of extremum is minimum, then the value of a isView SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
If the area bounded by f(x)=x33−x2+a and the straight lines x=0, x=2, and the x-axis is minimum, then the value of a isView Solution
Knowledge Check
- Question 1 - Select One
∫b+ca+cf(x)dx is equal to
A∫baf(x−c)dxB∫baf(x+c)dxC∫baf(x)dxD∫b−ca−cf(x)dx
1c∫bcacf(xc)dx=
View SolutionProve that ∫baf(x)dx=(b−a)∫10f((b−a)x+a)dx
View SolutionIf ∣∣∣∫baf(x)dx∣∣∣=∫ba|f(x)|dx,a<b,then f(x)=0 has
View SolutionProve that ∫baf(x)dx=∫b+ca+cf(x−c)dx , and when f(x) is odd function, ∫a−af(x)dx=0
View SolutionLet ∫baf(x)dx=∫b+ca+cf(x−c)dx. Then the value of ∫π0sin2010x⋅cos2009xdx is
View SolutionWhich of the following is incorrect? ∫b+ca+cf(x)dx=∫baf(x+c)dx ∫bcacf(x)dx=c∫baf(cx)dx ∫a−af(x)dx=12∫a−a(f(x)+f(−x)dx None of these
View Solution∫a0[f(x)+f(−x)]dx= (A) 0 (B) 2∫a0f(x)dx (C) ∫a−af(x)dx (D) none of these
View Solution

