If 1a:1b:1c=3:4:5, then a:b:c (a) 5:4:3 (b) 20:15:12 (c) 9:12:15 (d) 12:15:20
To solve the problem, we start with the given ratio:
1a:1b:1c=3:4:5
Step 1: Rewrite the ratio in terms of a, b, and c.
From the given ratio, we can express it as:
1a=3k,1b=4k,1c=5k
where k is a constant.
Step 2: Find expressions for a, b, and c.
To find a,b, and c, we take the reciprocal of each part:
a=13k,b=14k,c=15k
Step 3: Find a common denominator.
To express a,b, and c in a simpler ratio, we need a common denominator. The least common multiple (LCM) of the denominators (3, 4, and 5) is 60.
Step 4: Rewrite a, b, and c using the common denominator.
We can express a,b, and c as:
a=2060k,b=1560k,c=1260k
Step 5: Form the ratio a : b : c.
Now, we can write the ratio a:b:c as:
a:b:c=20:15:12
Conclusion: Identify the correct option.
The ratio a:b:c is 20:15:12, which corresponds to option (b).
Final Answer:
(b) 20:15:12
---
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If a:b=4:5,b:c=6:9,c:d=15:19, then a:b:c:d will be :
A8:10:15:19B10:11:15:19C8:9:15:19D19:15:6:8 - Question 2 - Select One
If a : b = 4 :5, b:c = 6 :9,c:d = 15:19, Find a : b : c : d
A8:10:15:19B10:11:15:19C8:9:15:19D19:15:6:8 - Question 3 - Select One
If cosθ=4/5, then (secθ+cosecθ) =
A. 7/5
B. 15/12
C. 35/12
D. 12/5AABBCCDD
3, 7, 6, 5, 9, 3, 12, 1, 15, (......) (a) 18 (b) 13 (c) -1 (d) 3
View SolutionIn Figure, the value of x is (a) 12 (b) 15 (c) 20 (d) 30
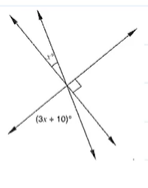 View Solution
View SolutionThree numbers are in the ratio 1 : 2 : 3 and their H.C.F. is 12. The numbers are (a) 4, 8, 12 (b) 5, 10, 15 (c) 10, 20, 30 (d) 12, 24, 36
View SolutionIf the arithmetic mean of 0, 5, 4, 3 is a , that of −1, 0, 1, 5, 4, 3 is b and that of 5, 4, 3 is c , then the relation between a, b and c is a=b=c (b) a:b:c=3:2:4 (c) 4a=5b=c (d) a+b+c=12
View SolutionThree numbers are in the ratio 1:2:3 and their HCF is 6, the numbers are 4, 8, 12 (b) 5, 10, 15 (c) 6, 12, 18 (d) 10, 20, 30
View Solution

