Question

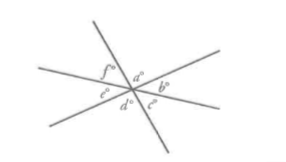
If $2s-e=32\text{and}2e-d=10$, what is the average of d and e?

Answer

21

Explanation

To solve the problem, we have the following two equations:

1. \( 2d - e = 32 \) (Equation 1)
2. \( 2e - d = 10 \) (Equation 2)

We need to find the average of \( d \) and \( e \), which is given by the formula:

\( \text{Average} = \frac{d + e}{2} \)

Step 1: Solve the equations simultaneously

Let's add the two equations together to eliminate one of the variables.

From Equation 1:
\( 2d - e = 32 \)

From Equation 2:
\( 2e - d = 10 \)

Adding these two equations:
\( (2d - e) + (2e - d) = 32 + 10 \)

Step 2: Simplify the left side

Combine like terms:
\( 2d - d + 2e - e = 32 + 10 \)

This simplifies to:
\( d + e = 42 \)

Step 3: Find the average of \( d \) and \( e \)

Now that we have \( d + e = 42 \), we can find the average:
\( \text{Average} = \frac{d + e}{2} = \frac{42}{2} = 21 \)

Final Answer

The average of \( d \) and \( e \) is \( 21 \).

---