If function h is defined by h(x)=ax2−7andh(−3)=29, what is h(12)?
−6
−5
4
8
The correct Answer is:A
To solve the problem step by step, we will follow these instructions:
1. Understand the function: We are given the function h(x)=ax2−7 and the condition h(−3)=29.
2. Substitute the value into the function: To find the value of a, we substitute x=−3 into the function:
h(−3)=a(−3)2−7=29
This simplifies to:
h(−3)=9a−7=29
3. Solve for a: Now, we will isolate a:
9a−7=29
Adding 7 to both sides gives:
9a=29+7
9a=36
Dividing both sides by 9:
a=369=4
4. Substitute a back into the function: Now that we have a=4, we can rewrite the function:
h(x)=4x2−7
5. Find h(12): We will now find the value of the function at x=12:
h(12)=4(12)2−7
This simplifies to:
h(12)=4⋅14−7
h(12)=1−7=−6
6. Final answer: Therefore, the value of h(12) is −6.
h(−3)=a(−3)2−7=29
This simplifies to:
h(−3)=9a−7=29
9a−7=29
Adding 7 to both sides gives:
9a=29+7
9a=36
Dividing both sides by 9:
a=369=4
h(x)=4x2−7
h(12)=4(12)2−7
This simplifies to:
h(12)=4⋅14−7
h(12)=1−7=−6
Topper's Solved these Questions
Similar Questions
Knowledge Check
Let a function of 2 variables be defined by h(x,y)=x2+3xy−(y−x), what is the value of h(5,4)?
A76B84C85D86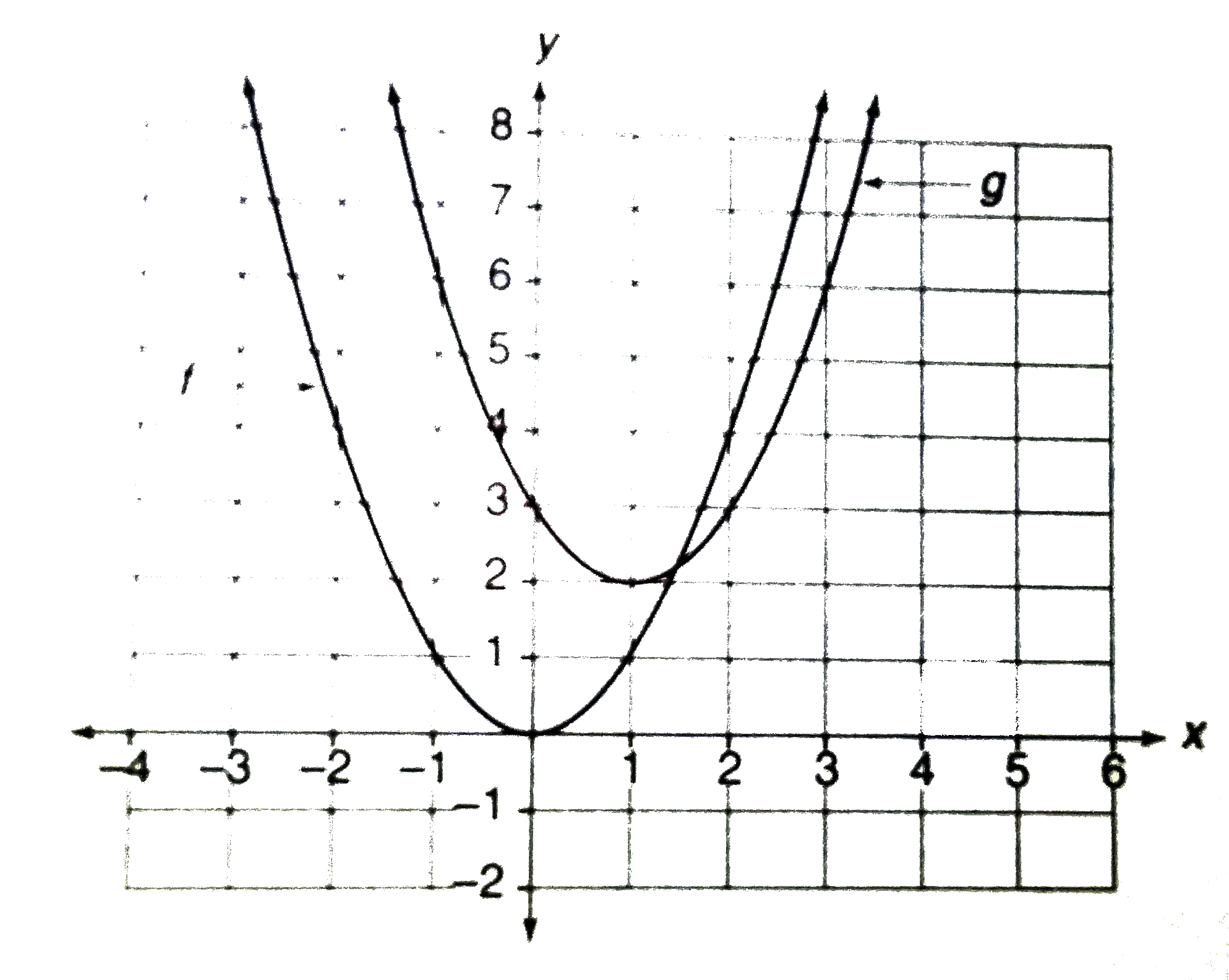
The accompanying figure shows the graphs of functions f and g. If f is defined by f(x)=x2 and g is defined by g(x)=f(x+h)+k, where h and k are constants, what is the value of h+k?A−3B−2C−1D1h(x)=2x
The function h is defined above. What is h(5) − h( 3) ?A2B4C24D28
A function satisfies g(5)=3 and g(3)=0, and a function h satisfies h(3)=-2 and h(0)=5.What is the value of h(g(3))?
View SolutionIf f, g, h are real functions defined by f=√x+1, g(x)=1x and h(x)=2x2−3, then find the values of (2fg+g−h)(1) and (2f+g−h)(1).
View Solutionh(x)=cx2+18
For the function h defined above, c is constant and h(2)=10. what is the value of h(-2)?
View SolutionLet the function h be defined by h(x)=√x+2. If 3h(v)=18, then which one of the following is the value of h(v4) ?
View SolutionLet the function q be defined by q(x)=a(x−h)2, where h is a positive constant, and a is a negative constant. For what value of x will the function q have its maximum value?
View Solution
