If 3 sin A = 4 cos A , find the value of :
tan2A−sec2A
The correct Answer is:−1
To solve the problem, we need to find the value of tan2A−sec2A given that 3sinA=4cosA.
1. Start with the given equation:
3sinA=4cosA
2. Rearrange the equation to find the ratio of sine to cosine:
sinAcosA=43
This implies:
tanA=43
3. Use the Pythagorean theorem to find the hypotenuse:
- In a right triangle, let the opposite side (perpendicular) be 4 and the adjacent side (base) be 3.
- The hypotenuse h can be calculated as:
h=√(42)+(32)=√16+9=√25=5
4. Calculate tan2A:
tan2A=(43)2=169
5. Calculate secA:
- The secant function is defined as:
secA=hypotenuseadjacent=53
6. Calculate sec2A:
sec2A=(53)2=259
7. Now substitute tan2A and sec2A into the expression tan2A−sec2A:
tan2A−sec2A=169−259
8. Combine the fractions:
tan2A−sec2A=16−259=−99=−1
9. Final answer:
tan2A−sec2A=−1
3sinA=4cosA
sinAcosA=43
This implies:
tanA=43
- In a right triangle, let the opposite side (perpendicular) be 4 and the adjacent side (base) be 3.
- The hypotenuse h can be calculated as:
h=√(42)+(32)=√16+9=√25=5
tan2A=(43)2=169
- The secant function is defined as:
secA=hypotenuseadjacent=53
sec2A=(53)2=259
tan2A−sec2A=169−259
tan2A−sec2A=16−259=−99=−1
tan2A−sec2A=−1
Topper's Solved these Questions
- TRIGONOMETRICAL RATIOS BOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS EXERCISE - EXERCISE 22(A)
47 Videos
- TRIGONOMETRICAL RATIOS BOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS EXERCISE - EXERCISE 22(B)
50 Videos
- TRIANGLES BOOK - ICSECHAPTER - TRIANGLES EXERCISE - 4 MARKS QUESTIONS
24 Videos
- TRIGONOMETRICAL RATIOS OF STANDARD ANGLESBOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS OF STANDARD ANGLESEXERCISE - EXERCISE 23(C)
118 Videos
Similar Questions
If 3 sin A = 4 cos A , find the value of :
sin A
View SolutionIf sin A = cos A, find the value of 2tan2A−2sec2A+5.
View SolutionIf 3 cos A = 4 sin A, find the value of :
3−cot2A+cosec2A
View SolutionIf cos A=4sinA, find the value of ,4cos2A−3sin2A+2
View SolutionIf sinθ=cosθ find the value of : 3tan2θ+2sin2θ−1
View SolutionIf secA=√2 , find the value of :
3cos2A+5tan2A4tan2A−sin2A
View SolutionFrom the following figure, find the values of :
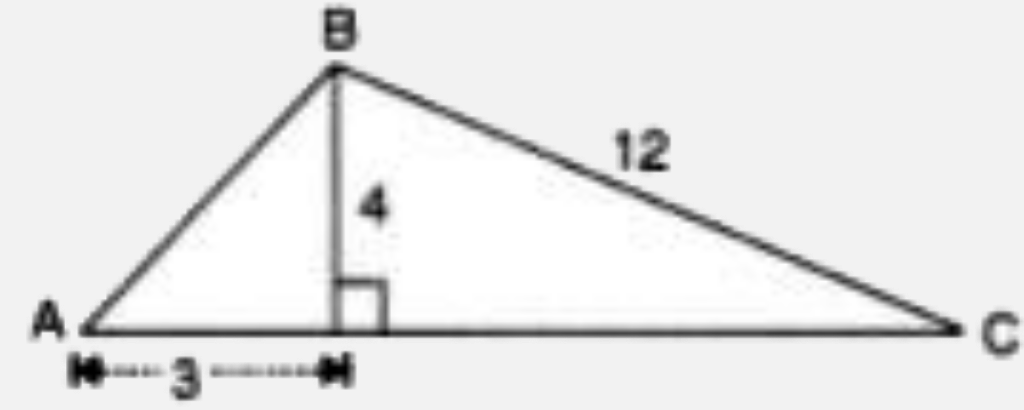
tan2A−sec2A
View SolutionIf cosA+cos2A=1, find the value of sin2A+sin4A.
View SolutionFind the value of : sec(cos−1(23))
View SolutionIf tanx=113 , find the value of : 4sin2x−3cos2x+2
View Solution
