In a triangle ABC, D is mid-point of BC, AD is produced upto E so that DE = AD. Prove that :
(i) ΔABDandΔECD are congruent.
(ii) AB = EC
(iii) AB is parallel to EC.
The correct Answer is:ΔABD≅ΔECD
Step by step video, text & image solution for In a triangle ABC, D is mid-point of BC, AD is produced upto E so that DE = AD. Prove that : (i) Delta ABD and Delta ECD are congruent. (ii) AB = EC (iii) AB is parallel to EC. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES Book:ICSEChapter:TRIANGLES Exercise:3 MARKS QUESTIONS
Explore 11 Videos
- STATISTICS AND GRAPH WORK Book:ICSEChapter:STATISTICS AND GRAPH WORK Exercise:TOPIC - 2 (4 Marks Questions)
Explore 14 Videos
- TRIGONOMETRICAL RATIOS Book:ICSEChapter:TRIGONOMETRICAL RATIOS Exercise:EXERCISE 22(B)
Explore 50 Videos
Similar Questions
In a ΔABC,D in mid-point of BC, AD is produced upto E so that DE=AD, prove that :
(i) ΔABD and ΔECD are congruent (ii) AB=EC
(iii) AB is parallel to EC.
View SolutionIn a triangle ABC,D is the mid - point of BC, AD is produced upto E so that DE = AD.
Prove that :
AB=EC
View SolutionIn a ΔABC, BD is the median to the side AC, BD is produced to E such that BD = DE. Prove that : AE is parallel to BC.
View SolutionIn isosceles triangle ABC, D is a point on the base BC produced. Prove that AD>AB.
View SolutionIn a triangle ABC,B=90∘ and D is the mid-oint of BC then prove that AC2=AD2+3CD2
View SolutionIn the given figure, DE // BC.

Prove that ΔADEandΔABC are similar
View SolutionAny point D is taken on the side BC of a ΔABC and AD is produced to E such that AD = DE , prove that area of ΔBCE= area of ΔABC,
View SolutionIn an isosceles triangle ABC, AB = AC and D is a point on BC produced. Prove that :
AD2=AC2+BD.CD
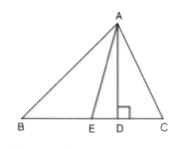
View SolutionIn triangle ABC, AB > AC. E is the mid-point of BC and AD is perpendicular to BC. Prove that : AB2+AC2=2AE2+2BE2
View SolutionIn a triangle ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that : AD = CE.
View Solution