If A = { (x,y) : y = sin x, x ∈ R } and B = { (x,y) : y = cos x, x ∈ R} then A ∩ B contains Solution in Tamil
no element
infinity many elements
only one element
cannot be determined.
The correct Answer is:A
Step by step video, text & image solution for If A = { (x,y) : y = sin x, x in R } and B = { (x,y) : y = cos x, x in R} then A cap B contains by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GOV. MODEL QUESTION PAPER - 1BOOK - SURA PUBLICATIONCHAPTER - GOV. MODEL QUESTION PAPER - 1EXERCISE - Section - II
10 Videos
- GOV. MODEL QUESTION PAPER - 1BOOK - SURA PUBLICATIONCHAPTER - GOV. MODEL QUESTION PAPER - 1EXERCISE - Section - III
11 Videos
- DIFFERENTIAL CALCUS - DIFFERENTIABILITY AND METHODS OF DIFFERENTIATIONBOOK - SURA PUBLICATIONCHAPTER - DIFFERENTIAL CALCUS - DIFFERENTIABILITY AND METHODS OF DIFFERENTIATIONEXERCISE - ADDITIONAL PROBLEMS SECTION-D (5 MARKS)
4 Videos
- GOVT. MODEL QUESTION PAPER - 2 (2018 - 19)BOOK - SURA PUBLICATIONCHAPTER - GOVT. MODEL QUESTION PAPER - 2 (2018 - 19)EXERCISE - SECTION - IV
13 Videos
Similar Questions
If A={1,2,3,4}andB={3,4,5,6}, find n((A∪B))×(A∩B)×(AΔB)).
View SolutionIf : R→R is defined by f(x) = 3x-5, prove that f is a bijection and find its inverse.
View SolutionIf y=√1+ex1−ex, show that dydx=ex(1−ex)√1−e2x.
View SolutionIf f,g:R→R are defined by f(x)=|x|−x, and g(x)=|x|−x, find g∘fandf∘g.
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
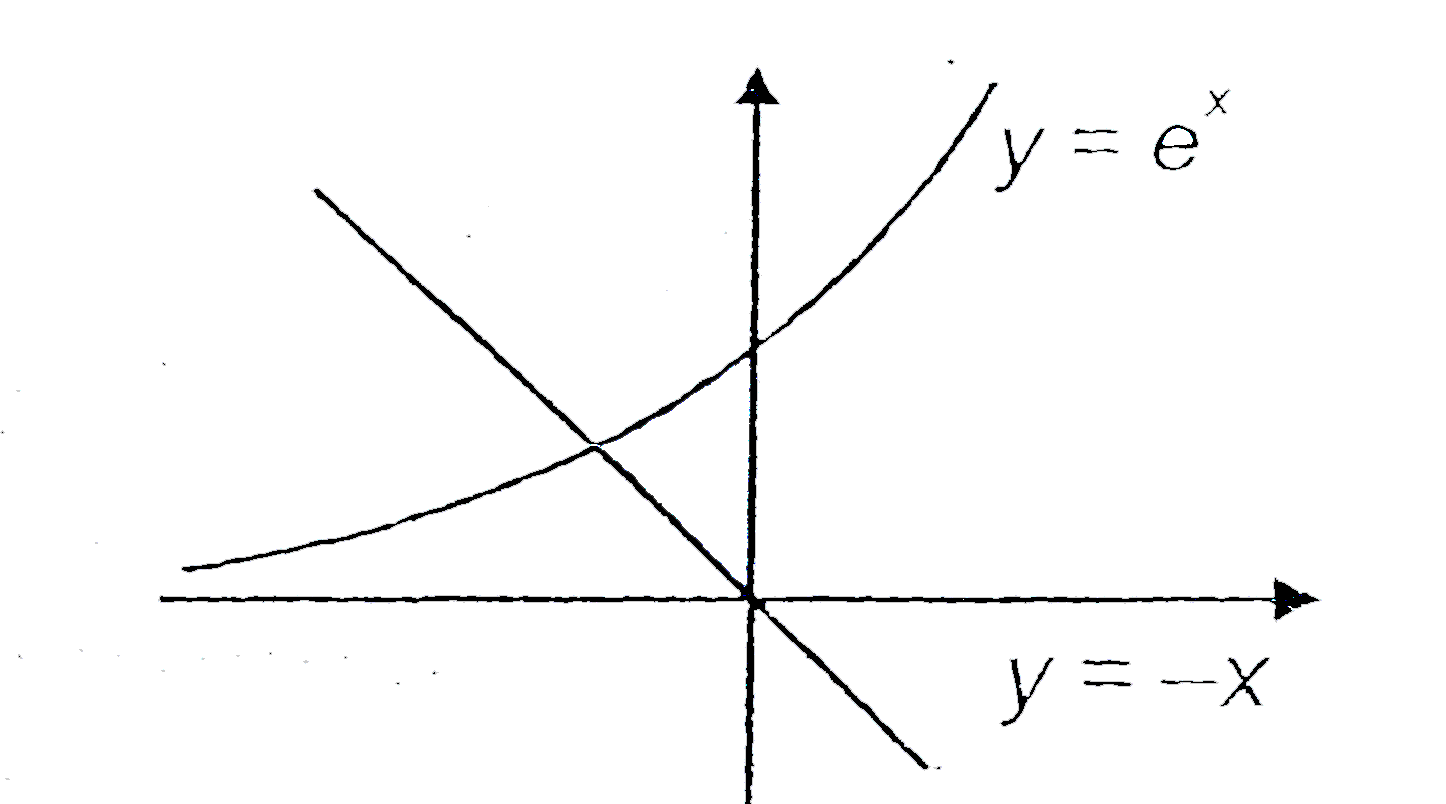
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A:{(x,y):y=√4−x2,x∈[−2,2]}
B={(x,y):y=|x|,x∈R}
Then n(A∩B)
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
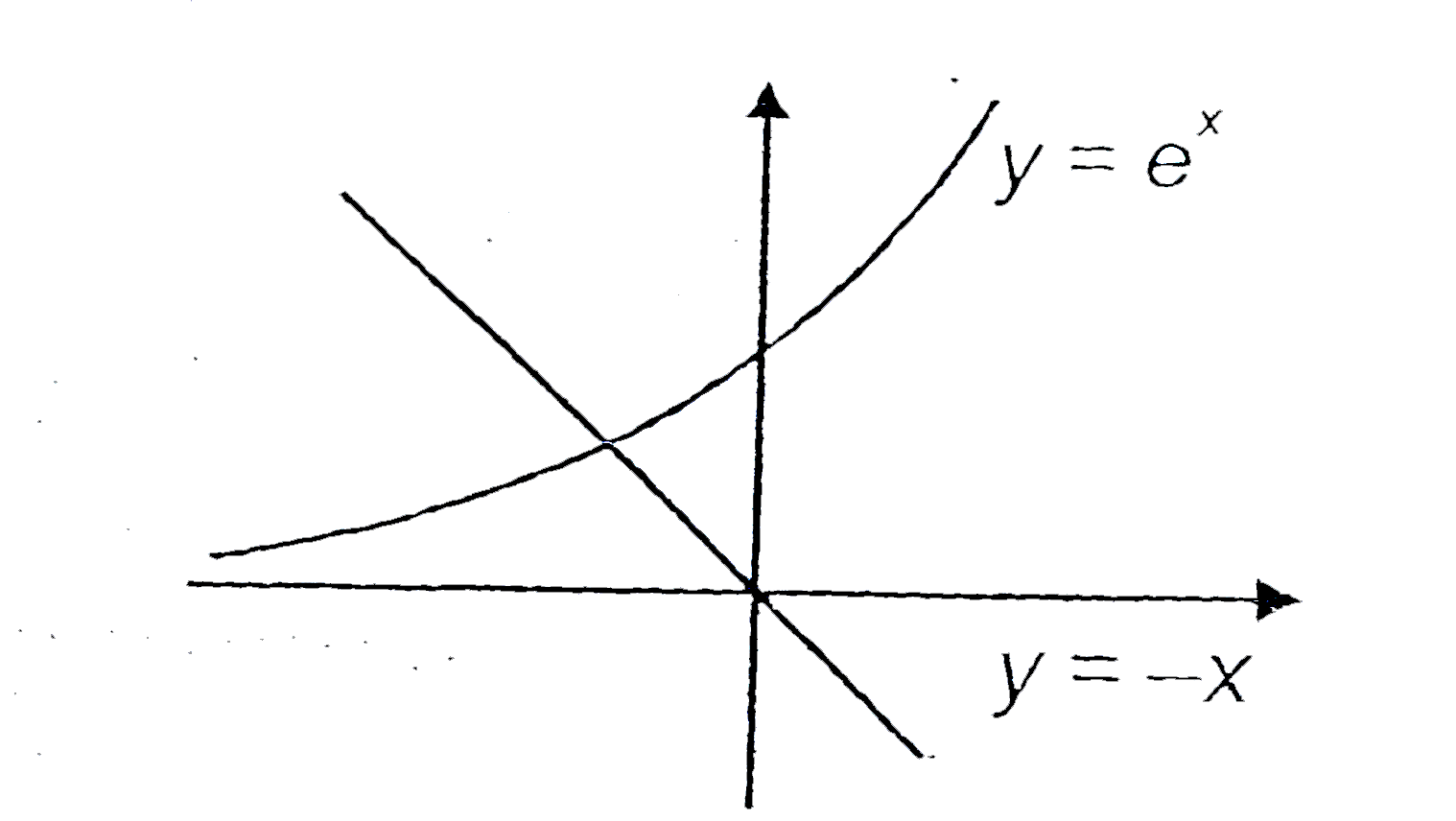
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):x2+y2≤2,x,y∈R}
B={{x,y):y≥x2,x,y∈R}
Then domain of A∩B is
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
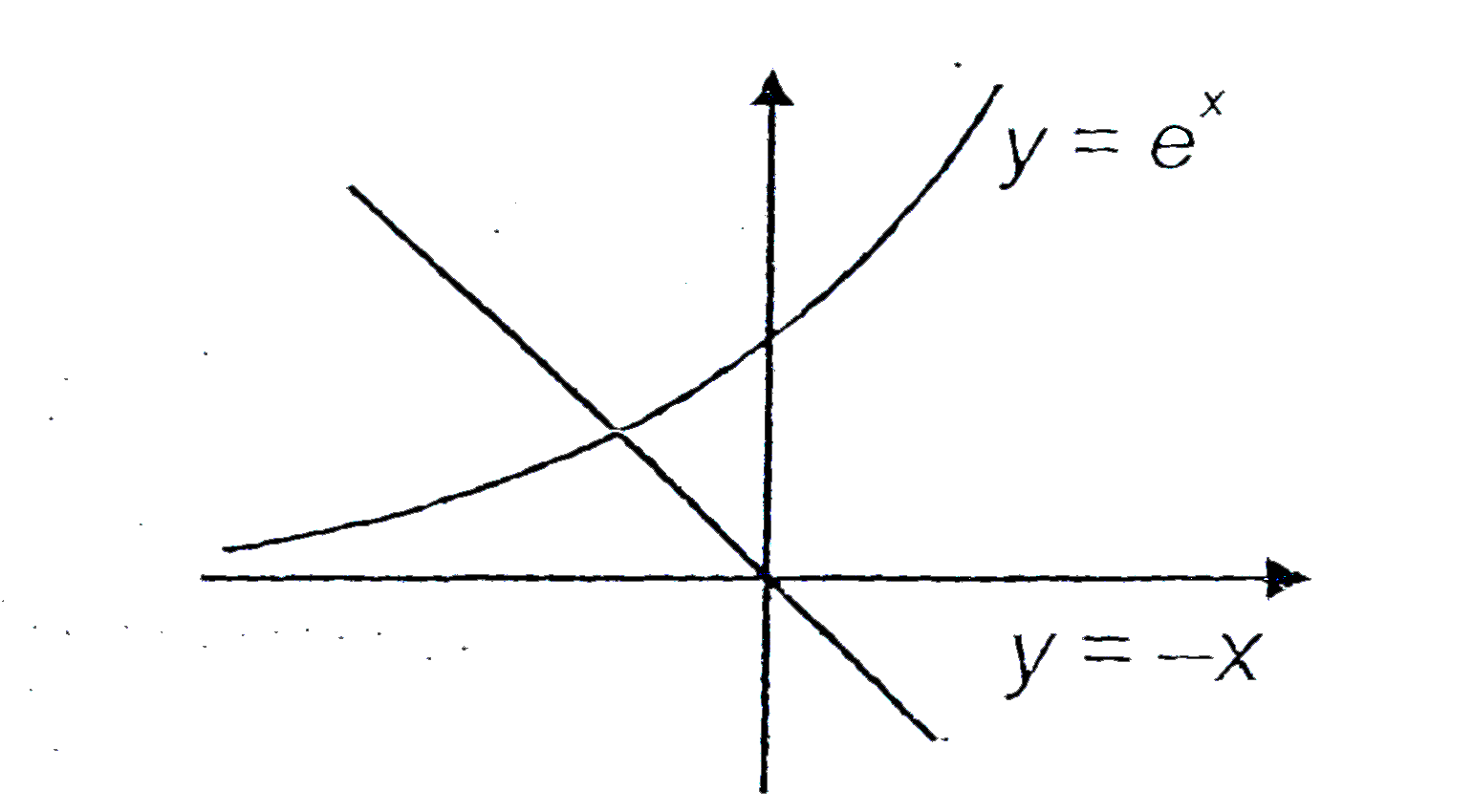
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):y=sinπx,x∈R}
B={(x,y):y=|In|x||,x∈R−{0}}
Then, n(A∩B)
View SolutionLet A={(x,y):y=ex,x∈R}B={(x,y),Y=e−x,x∈R}then
View SolutionIf A= {(x,y) : y = ex,x∈R} and B = { (x,y) : y = e−x,x∈R } then n (A ∩ B ) is
View SolutionIf A = { (x,y) : y = sin x, x ∈ R } and B = { (x,y) : y = cos x, x ∈ R} then A ∩ B contains
View SolutionA={(x,y):y=1/x,0≠x∈R},B={(x,y):y=−x,x∈R} then
View SolutionA={(x,y):y=ex,x∈R},B={(x,y):y=x,x∈R} then
View SolutionLet A={(x,y): y=ex,x∈R } , B={(x,y): y= e−x,x∈R } . Then :
View SolutionLet A={(x,y : y=ex,x∈R} , B={(x,y): y=x, x ∈ R} . Then :
View SolutionThe number of elements in the set A∩B∩C, where
A={(x,y)∈R×R,|x|+|y|≥1}
B={(x,y)∈R×R,x2+y2≥1}
and C={(x,y)∈R×R: max |x|,|y|=1} is:
View SolutionLet A={(x,y)/y=ex,x∈R},B={(x,y)/y=e−x,x∈R}, then
View Solution
