If A and B are the points of intersection of y=f(x) and y=f−1(x), then
A and B necessarity lie on the line y=x
A and B must be coincident
slope of line AB may be -1
None of these above
The correct Answer is:C
To solve the problem, we need to analyze the points of intersection of the functions y=f(x) and y=f−1(x).
1. Understanding the Functions:
- The function y=f(x) represents a function.
- The function y=f−1(x) represents the inverse of that function.
2. Points of Intersection:
- The points of intersection A and B occur where f(x)=f−1(x).
- This means we are looking for values of x such that f(x)=x.
3. Analyzing the Graphs:
- The line y=x is the line of symmetry for the function and its inverse.
- If a point (a,b) is on the line y=f(x), then the corresponding point on the inverse function will be (b,a).
4. Slope of Line AB:
- The slope of the line connecting points A and B (where A and B are the intersection points) can be determined.
- If A=(a,f(a)) and B=(b,f(b)), then the slope of line AB is given by:
slope=f(b)−f(a)b−a
- Since f(a)=f−1(a) and f(b)=f−1(b), we can infer that the slope of line AB will be -1 if f(x) is a function that is symmetric about the line y=x.
5. Conclusion:
- The points of intersection A and B will lie on the line y=x if f(x) is such that f(x)=x at those points.
- The line connecting points A and B will have a slope of -1, indicating that the inverse function reflects across the line y=x.
Final Result:
- The points of intersection A and B of the functions y=f(x) and y=f−1(x) will satisfy the property that the slope of the line connecting these points is -1.
- The function y=f(x) represents a function.
- The function y=f−1(x) represents the inverse of that function.
- The points of intersection A and B occur where f(x)=f−1(x).
- This means we are looking for values of x such that f(x)=x.
- The line y=x is the line of symmetry for the function and its inverse.
- If a point (a,b) is on the line y=f(x), then the corresponding point on the inverse function will be (b,a).
- The slope of the line connecting points A and B (where A and B are the intersection points) can be determined.
- If A=(a,f(a)) and B=(b,f(b)), then the slope of line AB is given by:
slope=f(b)−f(a)b−a
- Since f(a)=f−1(a) and f(b)=f−1(b), we can infer that the slope of line AB will be -1 if f(x) is a function that is symmetric about the line y=x.
- The points of intersection A and B will lie on the line y=x if f(x) is such that f(x)=x at those points.
- The line connecting points A and B will have a slope of -1, indicating that the inverse function reflects across the line y=x.
- The points of intersection A and B of the functions y=f(x) and y=f−1(x) will satisfy the property that the slope of the line connecting these points is -1.
Topper's Solved these Questions
- FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - FUNCTIONSEXERCISE - Exercise For Session 1
5 Videos
- FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - FUNCTIONSEXERCISE - Exercise For Session 2
6 Videos
- ESSENTIAL MATHEMATICAL TOOLS BOOK - ARIHANT MATHS ENGLISHCHAPTER - ESSENTIAL MATHEMATICAL TOOLS EXERCISE - Exercise (Single Integer Answer Type Questions)
3 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
10 Videos
Similar Questions
Statement -1 All points of intersection of y=f(x) and y=f−1(x) lies on y=x only.
Statement -2 If point P(α,β) lies on y=f(x) then Q(β,α) lies on y=f−1(x).
Statement -3 Inverse of invertible function is unique and its range is equal to the function domain.
Which of the following option is correct for above statements in order
View SolutionLet a differentiable function f:R→R be such that for all x and y in R
2|f(x)−f(y)|≤|x−y| and f′(x)≥12. So then the number of points of intersection of the graph y=f(x) with
View SolutionThe point of intersection of the lines xa+yb=1 and xb+ya=1 lies on
View SolutionStatement I- Area bounded by y=x(x−1) and y=x(1−x)is13.
Statement II- Area bounded by y=f(x) and y=g(x) "is" ∣∣∣∫ba(f(x)−g(x))dx∣∣∣ is true when f(x) and g(x) lies above X-axis.(Where a and b are intersection of y=f(x)andy=g(x)).
View SolutionConsider the function f(x)={2x+3,x≤1and−x2+6,x>1} Then draw the graph of the function y=f(x),y=f(|x|)andy=|f(x)|.
View SolutionConcavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)

Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)
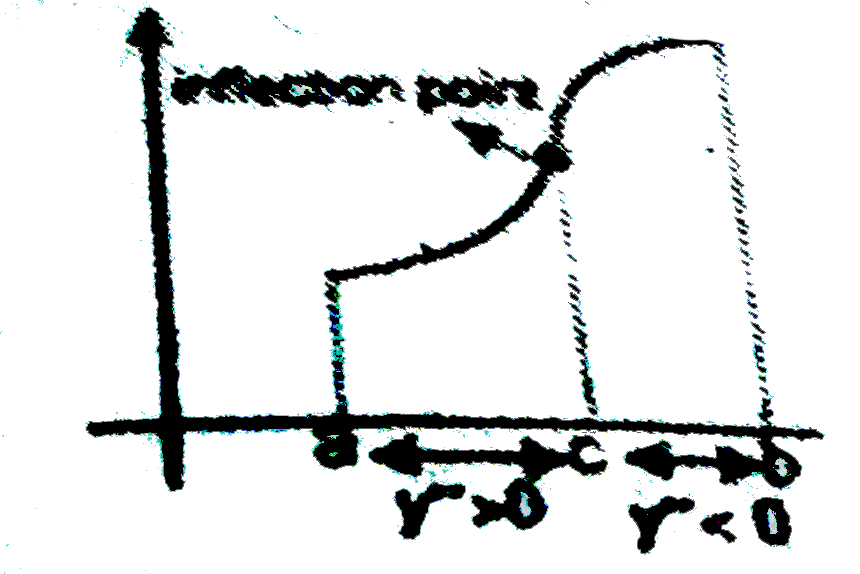
Number of point of inflection for f(x)=(x−1)3(x−2)2 is :
View SolutionStatement-1 : The third law of thermodynamics implies that absolute zero cannot be reached.
Statement-2 : ΔG∘ for an ideal gas reaction is a function of temperature.
Statement-3 : The adiabatic expansion of a gas into a vacuum is spontaneous.
View SolutionFind the point of intersection of the tangents drawn to the curve x2y=1−y at the points where it is intersected by the curve xy=1−y.
View SolutionWe say an equation f(x)=g(x) is consistent, if the curves y=f(x)andy=g(x) touch or intersect at atleast one point. If the curves y=f(x)andy=g(x) do not intersect or touch, then the equation f(x)=g(x) is said to be inconsistent i.e. has no solution.
The equation sinx=x2+x+1 is
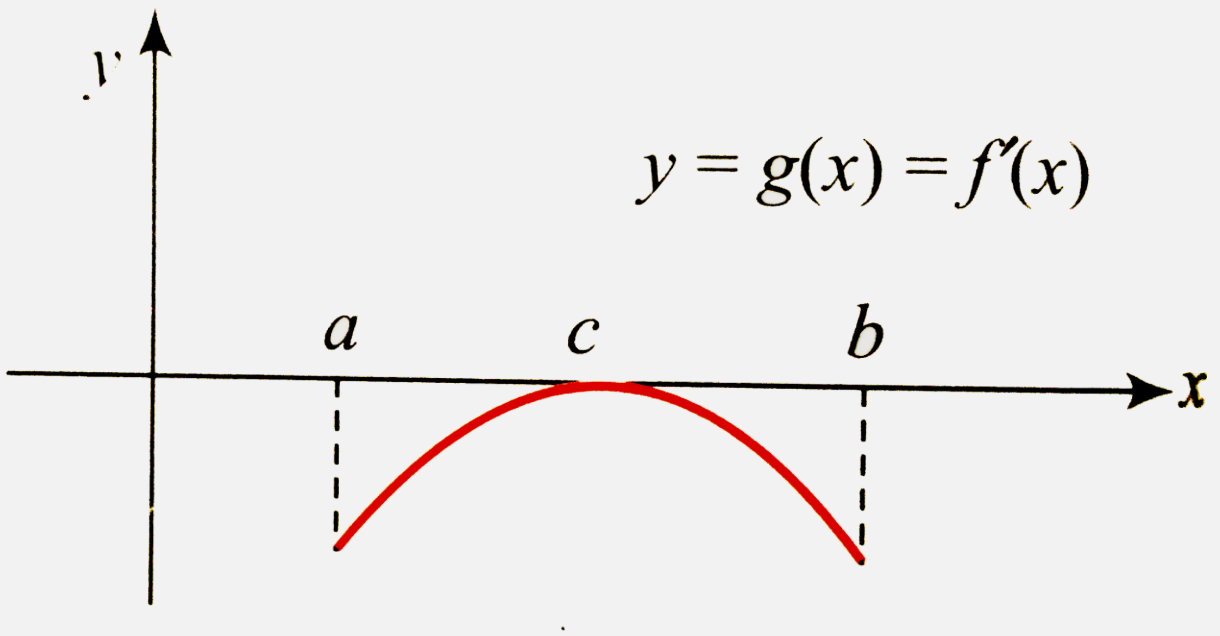
View SolutionFollowing is the graph of y = f' (x) , given that f(c) = 0. Analyse the graph and answer the following questions.
(a) How many times the graph of y = f(x) will intersect the x - axis?
(b) Discuss the type of roots of the equation f (x) = 0, a≤x≤b.
(c) How many points of inflection the graph of y=f(x),a≤x≤b, has?
(d) Find the points of local maxima/minima ofy=f(x),a<xb.
(e) How many roots equation f''(x)=0 has?
View Solution
