If a ∈ R and the equation −3(x−[x]2)+2(x−[x])+a2=0 (where [x] denotes the greatest integer ≤x) has no integral solution,then all possible values of a lie in the interval :Solution in Bengali
(−1,0)∪(0,1)
(1,2)
(−2,−1)
(−∞,−2)∪(2,∞)
The correct Answer is:A
a2=3t2−2t, where t={x}∈[0,1)
∴a2=3t(t−2/3)
Graph of f(t)=3t(t−2/3) is as shown in the following figure.
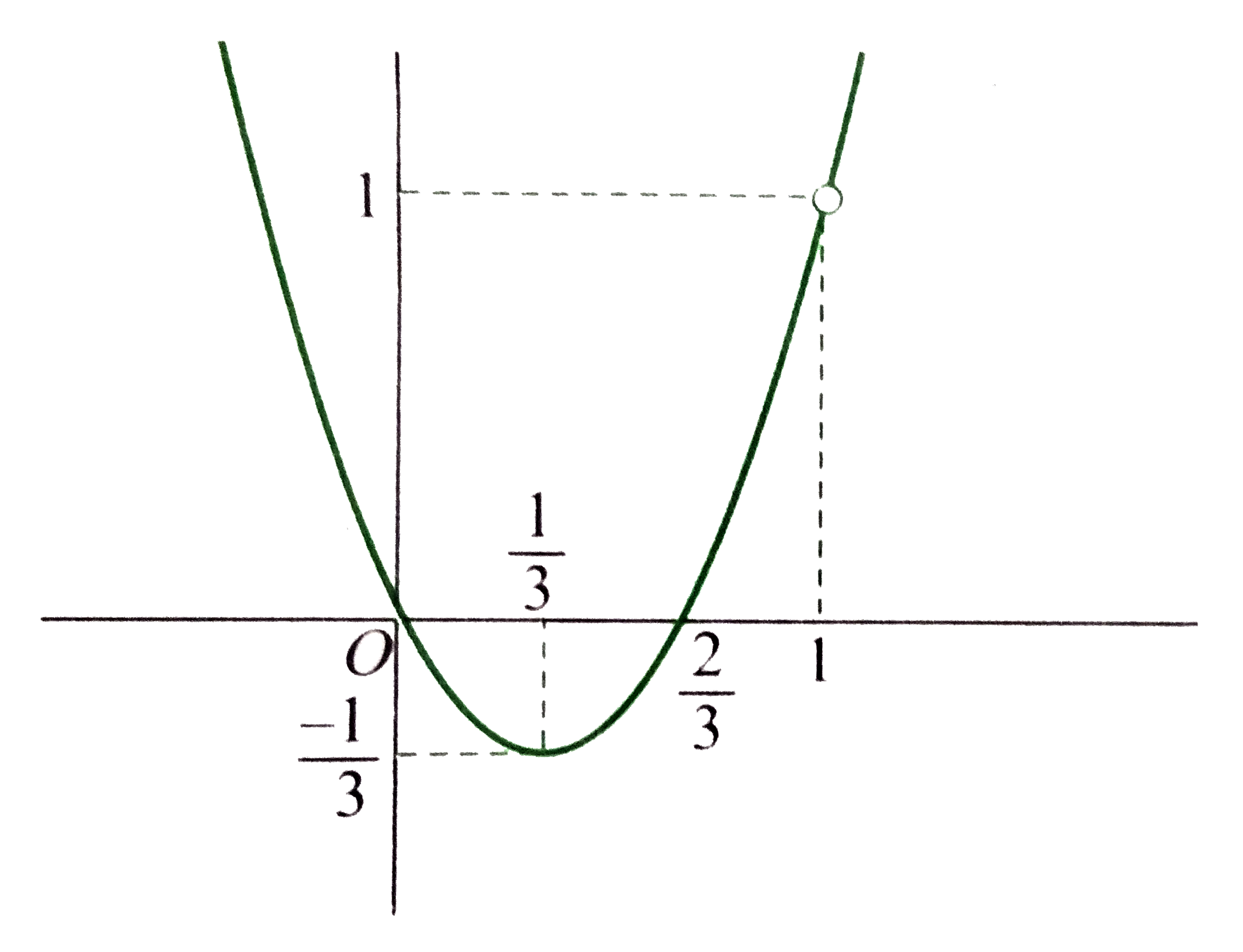
Clearly, from graph
0<a2<1
ora∈(−1,0)∪(0,1)
Topper's Solved these Questions
Similar Questions
Let ABCandABC' be two non-congruent triangles with sides AB=4,AC=AC′=2√2 and angle B=300 . The absolute value of the difference between the areas of these triangles is
View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj−ˆk and ˆi−ˆj+ˆk, in the order form right-handed system ∀x ∈R, is
(a) 0 (b) 2 (c) 4 (d) 6
View SolutionIf a in R and the equation -3(x-[x])^2+""2""(x-[x])""+a^2=""0 (where [x] denotes the greatest integer x) has no integral solution, then all possible values of a lie in the interval (1) (-1,""0)uu(0,""1) (2) (1, 2) (3) (-2,-1) (4) (-oo,-2)uu(2,oo)
View SolutionIf a in R and the equation -3(x-[x])^2+2(x-[x])+a^2=0 (where [x] denotes the greatest integer le x) has no integral solution, then all possible values of a lie in the interval: (1) (-2,-1) (2) (oo,-2) uu (2,oo) (3) (-1,0) uu (0,1) (4) (1,2)
View SolutionLet [x] denote the greatest integer in x .Then in the interval [0,3] the number of solutions of the equation,x^(2)-3x+[x]=0 is
View SolutionIf a ∈ R and the equation (a−2)(x−[x])2+2(x−[x])+a2=0 (where [x] denotes the greatest integer function) has no integral solution and has exactly one solution in (2, 3), then a lies in the interval
View SolutionIF ∈R and the equation −3(x−[x])+a2=0 ( where [x] denotes the greatest ineteger ≤x ) has no integral solution , then all possible values of a lie in the interval
View SolutionIf ain RR and the equation -3(x-[x])^2+2(x-[x])+a^2=0 (where [x] denotes the greatest integer lex) has no integral solution, then all possible values of a lie in the interval____
View Solutionयदि a∈R तथा समीकरण −3(x−[x])2+2(x−[x])+a2=0 (जहाँ, [x] उस बड़े से पूर्णांक को दर्शाता है जो ≤x है) का कोई पूर्णांकीय हल नहीं है, तो a के सभी सम्भव मान जिस अन्तराल में स्थित है, वह है
View SolutionIf ainR and the equation -3(x-[x])^(2)+2(x-[x])+a^(2)=0 , (where [x] denotes the greatest integer le x) has no integral solution, then all possible values of a lie in the interval :
View SolutionIf a in R And equation -3(x-[x])^(2)+2(x-[x])+a^(2)=0 (Where, [x] represents the largest integer that le x Is), there is no integer solution, then the interval in which all possible values of a is located is
View SolutionIf [x] denotes the greatest integer ≤x , then number of solutions of the equation x2−2−2[x]=0 is
View SolutionIf a in R and the equation -3(x-[x])^2+2(x-[x])+a^2=0 (where [x] denotes the greatest integer le x ) has no integral solution, then all possible values of a lie in the interval: (1) (-2,-1) (2) (oo,-2) uu (2,oo) (3) (-1,0) uu (0,1) (4) (1,2)
View SolutionIf a in R and the equation -3(x-[x]^2)+2(x-[x])+a^2=0 (where [x] denotes the greatest integer le x) has no integral solution,then all possible values of a lie in the interval :
View SolutionThe number of integral values of n (where n>=2) such that the equation 2n{x} = 3x + 2[x] has exactly five solutions (where [.] denotes the greatest integer function and {x} denotes the fractional part of x) is
View SolutionIf a ∈ R and the equation (a−2)(x−[x])2+2(x−[x])+a2=0 (where [x] denotes the greatest integer function) has no integral solution and has exactly one solution in (2, 3), then a lies in the interval
View Solution
