If a line intersects sides AB and AC of a ΔABCat D and E respectively and is parallel to BC, prove that ADAB=AEAC
∠ADE~∠ABC (AAA)
ADAB=DEBC=AEAC
ABAD=ACEA
AD+DBAD=AE+ECAE
1+DBAD=1+ECAC
DBAD=ECAC
Similar Questions
If a line intersects sides AB and AC of a ΔABCat D and E respectively and is parallel to BC, prove that ADAB=AEAC
View SolutionThe vertices of ABC are A(4, 6), B(1, 5) and C(7, 2) . A line is drawn to intersect sides AB and AC at D and E respectively such that ADAB=AEAC=14 . Calculate the area of ADE and compare it with the area of ABC .
View Solution
Knowledge Check
A straight line parallel to the base BC of the triangle ABC intersects AB and AC at the points D and E respectively. If the area of the ΔABE be 36 sq. cm, then the area of the ΔACD is
A18 sq. cmB36 sq. cmC18 cmD36 cmIn triangle ABC , sides AB and AC are extended to D and E, respectively, such that AB=BD and AC =CE,F∈dDE,ifBC=6 cm.
A3 cmB6cmC9 cmD12 cm
The vertices of a ΔABCareA(4,6),B(1,5)andC(7,2). A line is drawn to intersect side AB and AC at D and E respectively, such that ADAB=AEAC=14. Calculate the area of ΔADE and compare it with the area of ΔABC.
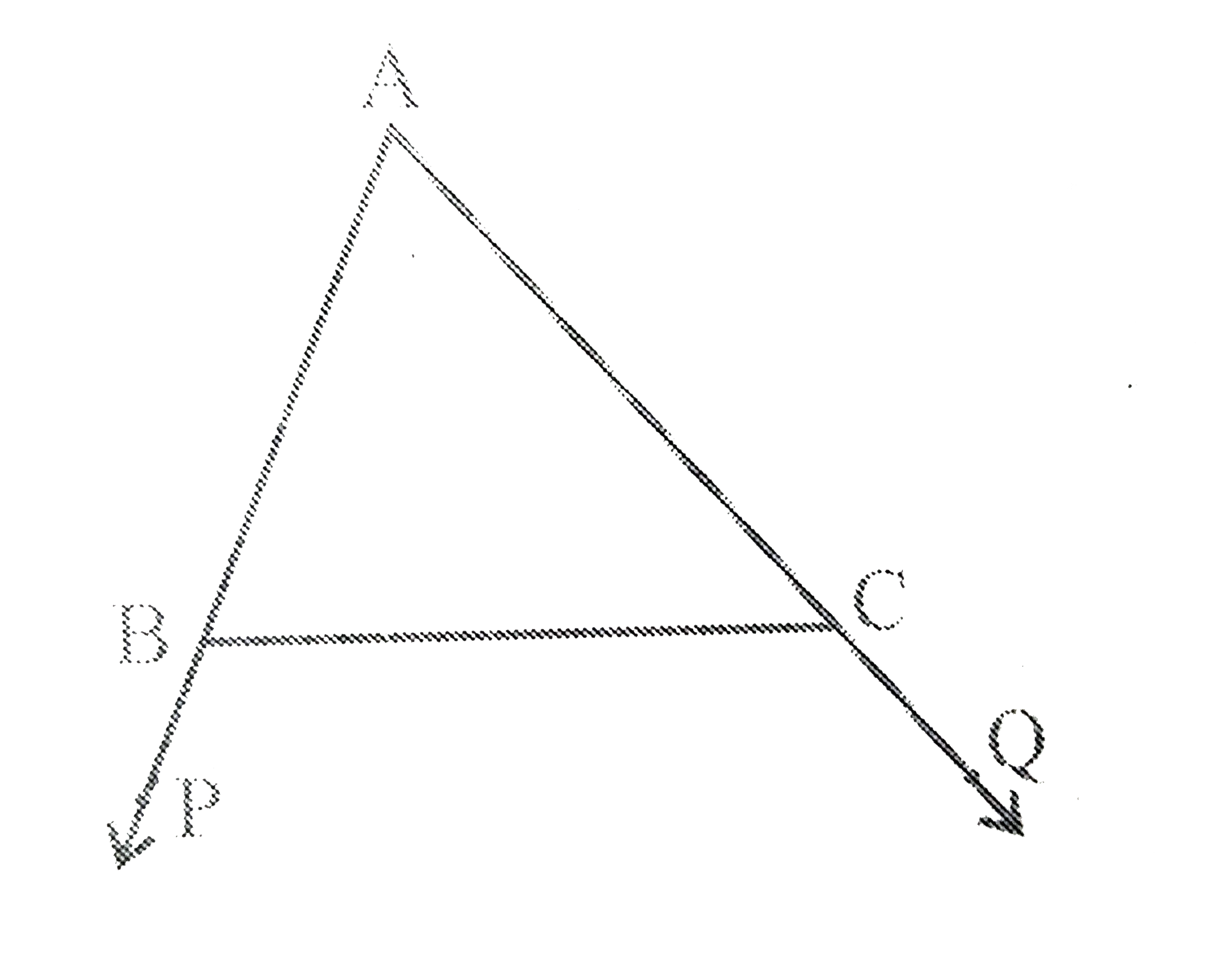
View SolutionIn Fig. 7.48, sides ABandAC of ΔABC are extended to points PandQ respectively. Also, ∠PBC <∠QCB. Show that AC > AB.
View SolutionA triangle ABC (with usual notations) is a right angled isosceles triangle right angled at B. Let a line isdrawn passing through the centroid 'G' of the triangle and parallel to BC intersecting sides ABandAC at DandE respectively, if length of BC=9, then the area of quadrilateral ADGF (where F is the midpoint of AC) is
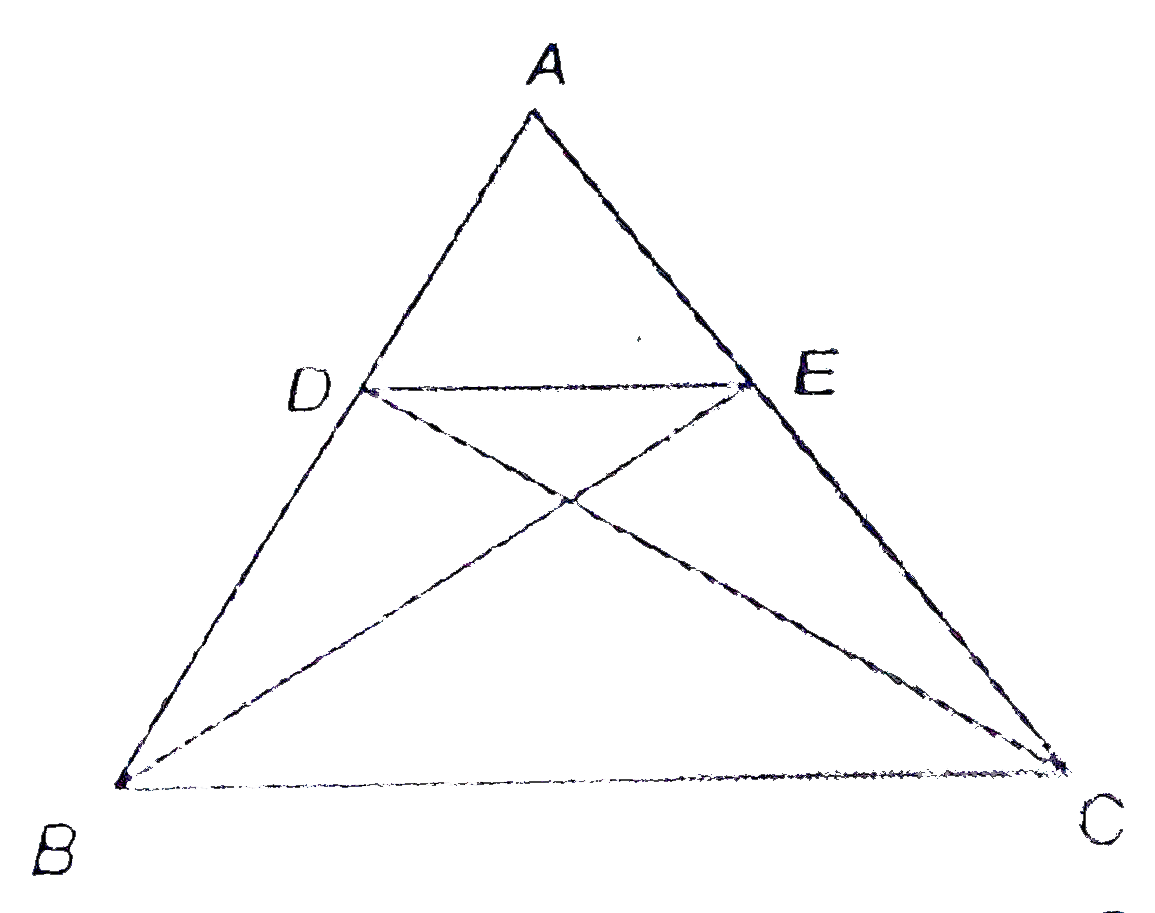
View SolutionD and E are points on sides AB and AC respectively of ΔABC such that ar(ΔDBC) = ar(ΔEBC). Prove that DE I I BC.
View SolutionIn the adjoning figure, D and E are the points on the sides AB and AC respectively of ΔABC and area of ΔBCE= area of ΔBCD.
Prove that DE∣∣BC
View SolutionIf A, B and C are three points on a line, and B lies between A and C (see figure), then prove that AB + BC = AC.

View Solution
