Question

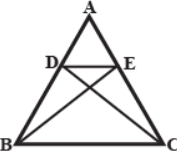
D and E are points on sides AB and AC respectively of $\Delta$ABC such that ar($\Delta$DBC) = ar($\Delta$EBC). Prove that DE I I BC.

Explanation

To prove that line segment DE is parallel to line segment BC in triangle ABC, given that the areas of triangles DBC and EBC are equal, we can follow these steps:

1. Understand the Given Information:
We have triangle ABC with points D and E on sides AB and AC respectively. We are given that the area of triangle DBC is equal to the area of triangle EBC.

2. Write Down the Area Condition:
We know that:
\( \text{ar}(\Delta DBC) = \text{ar}(\Delta EBC) \)

3. Identify the Common Base:
Both triangles DBC and EBC share the same base BC.

4. Use the Area Formula:
The area of a triangle can be expressed as:
\( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \)
For triangles DBC and EBC, we can express their areas as:
\( \text{ar}(\Delta DBC) = \frac{1}{2} \times BC \times h_D \)
\( \text{ar}(\Delta EBC) = \frac{1}{2} \times BC \times h_E \)
where \( h_D \) and \( h_E \) are the heights from points D and E to line BC respectively.

5. Set the Area Equations Equal:
Since the areas are equal, we can set the two area equations equal to each other:
\( \frac{1}{2} \times BC \times h_D = \frac{1}{2} \times BC \times h_E \)

6. Simplify the Equation:
Since \( BC \) is the same in both equations and is not equal to zero, we can divide both sides by \( \frac{1}{2} \times BC \):
\( h_D = h_E \)

7. Interpret the Heights:
The equality \( h_D = h_E \) means that the perpendicular distances from points D and E to line BC are equal.

8. Conclude the Parallelism:
Since D and E are at the same height from line BC, by the properties of parallel lines, we can conclude that line DE is parallel to line BC:
\( DE \parallel BC \)

Final Statement:
Thus, we have proved that DE is parallel to BC.

---