If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
Video Solution
Text Solution
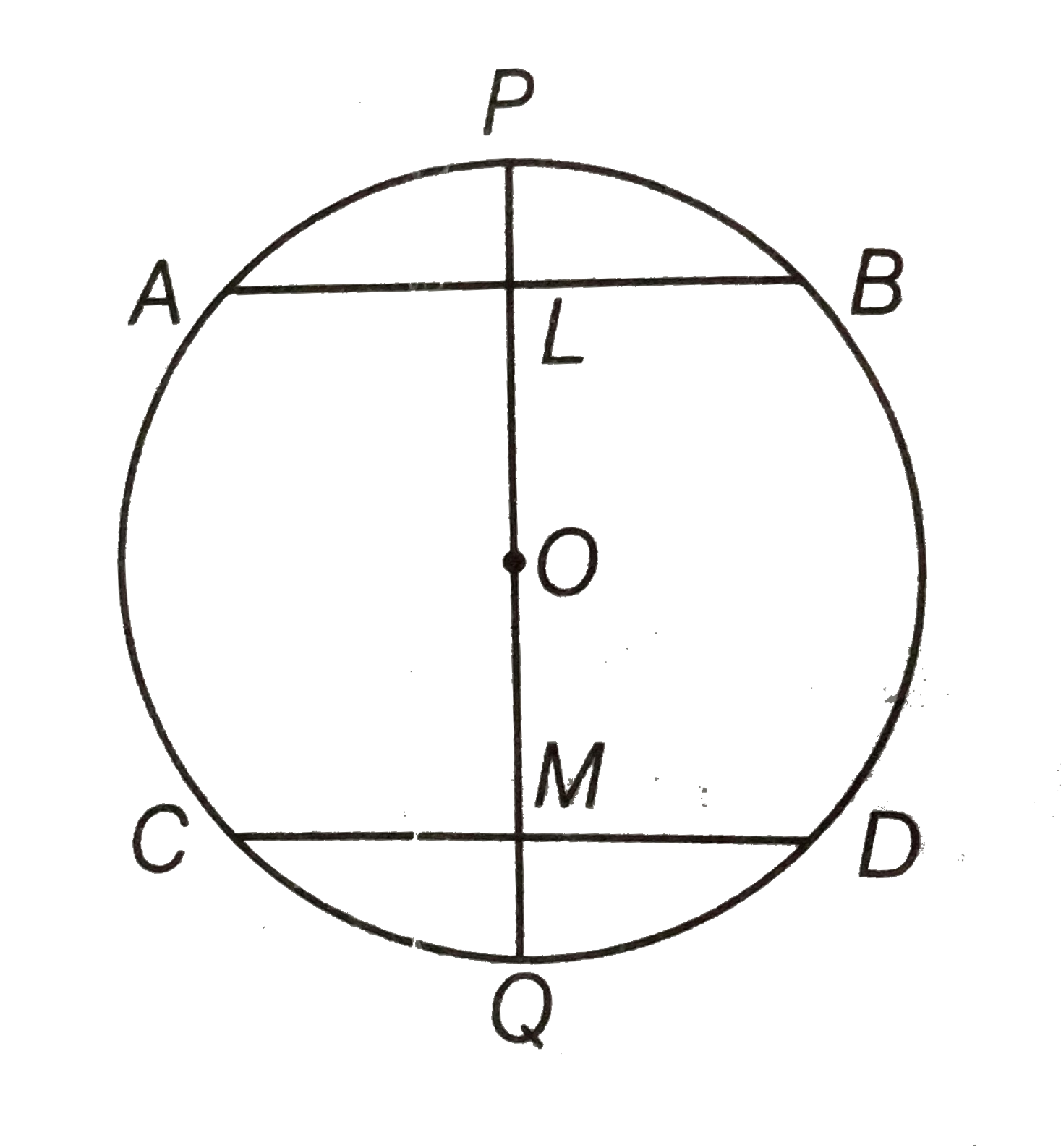
Given AB and CD are two chords of a circle whose centre is O and PQ is a diameter bisecting the chord AB and CD at L and M, respectively and the diameter PQ passes through the centre O of the circle.
To prove AB∣∣CD
Proof Since, L is the mid-point of AB.
∴OL⊥AB
[since, the line joining the centre of a circle to the mid-point of a chord is perpendicular to the chord]
⇒∠ALO=90∘....(i)
Similarly, OM⊥CD...(ii)
From Eqs. (i) and (ii) ∠ALO=∠OMD=90∘
But, these are alternating angles.
So, AB∣∣CD
|
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.4
2 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles
34 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
Knowledge Check
A chord that passes through the centre of a circle is___
ADiameterBSegmentCRadiusDCentreThe chord of a circle which passes through the centre is___the radius
AThriceBDoubleCHalfDEqual to
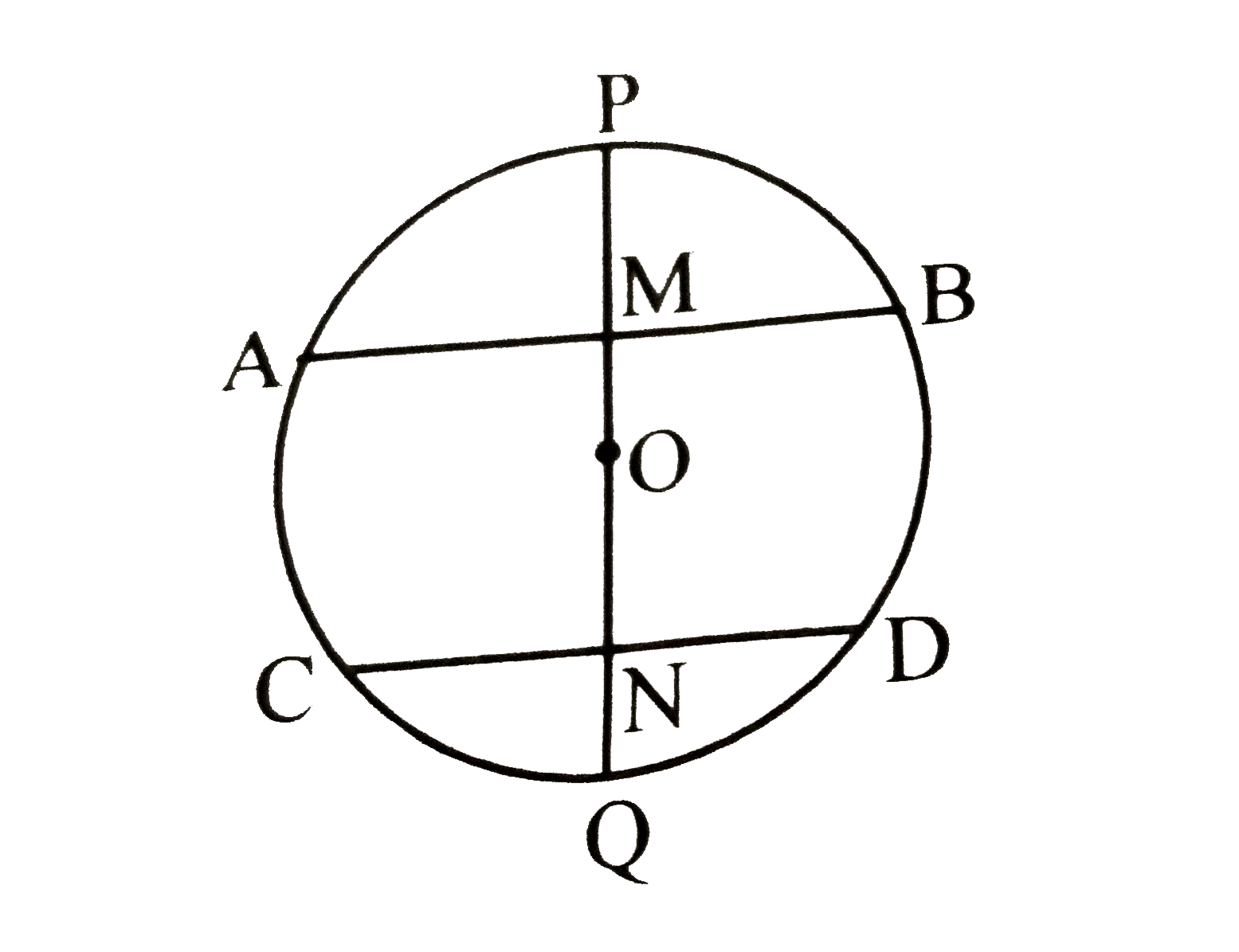
If a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
View SolutionProve that, if a diameter of a circle bisects two chords of the circle then those two chords are parallel to each other.
View Solution
The chord, which passes through the centre of the circle, is called a ........... of the circle.
View SolutionProve that the perpendicular bisector of a chord of a circle always passes through the centre.
View SolutionProve that the segment joining the point of contact of two parallel tangents passes through the centre.
View SolutionProve that the line segment joining the mid points of two sides of a triangle is parallel to its third side.
View Solution
