A triangle if its perimeter is 10.4cm and two angles are 45∘and120∘ .
Let ABC be a triangle. Then, given perimeter = 10.4cm i.e., AB+BC+CA=10.4cm and two angles are 45∘and120∘ .
say ∠B=45∘and∠C=120∘
Now, to construct the ΔABC use the following steps.
(i) Draw a line segment say XY and equal to perimeter i.e., AB+BC+CA=10.4cm (ii) Make angle ∠LXY=∠B=45∘and∠MYX=∠C=120∘.
(iii) Bisect ∠LXYand∠MYX and let these bisectors intersect at a point A (say).
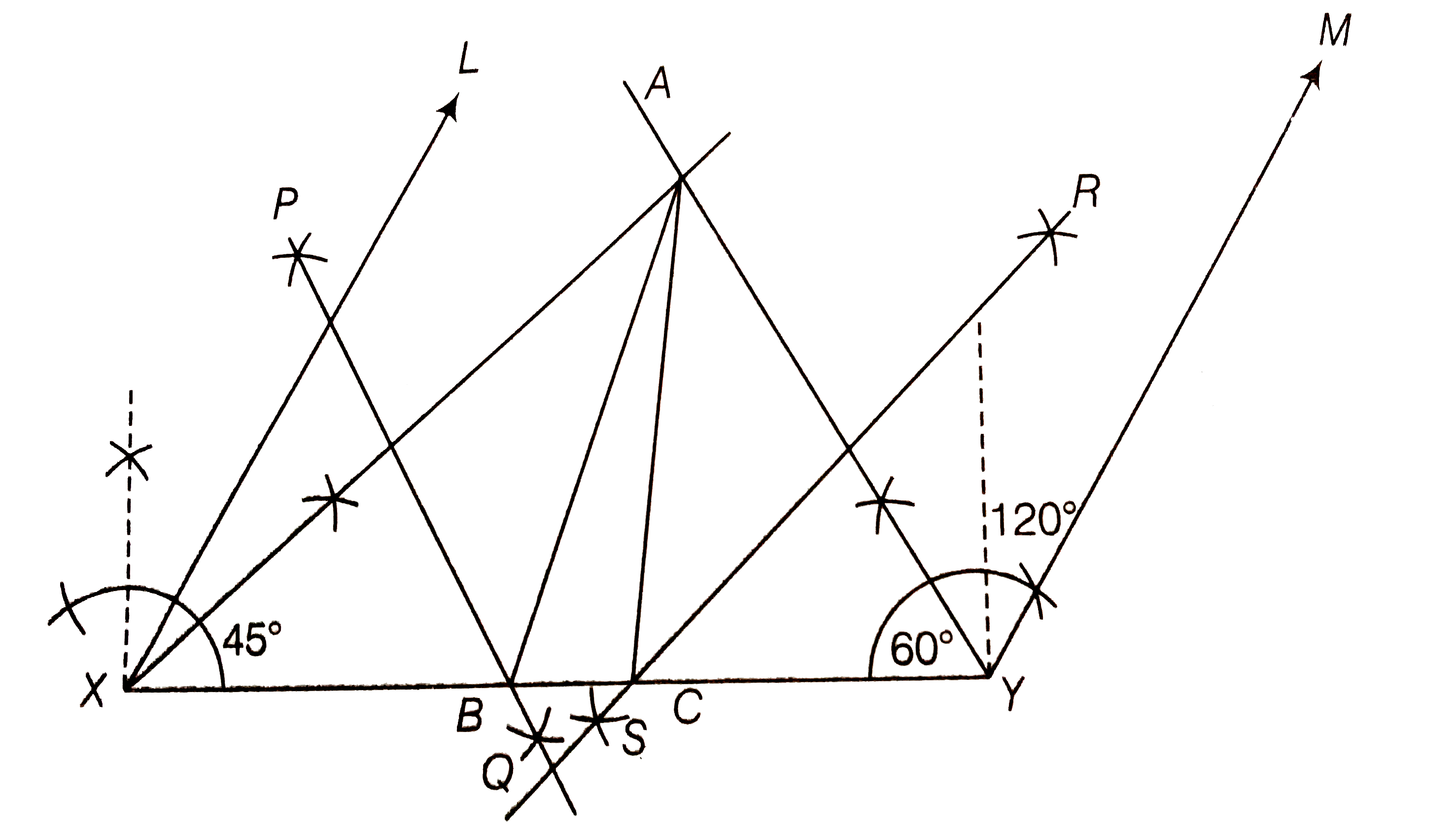
(iv) Draw perpendicular bisectors PQ and RS of AX and AY, respectively.
(v) Let PQ intersect XY at B and RS intersect XY at C. Join AB and AC. Thus , ΔABC is the required triangle.
Justification Since, B lies on the perpendicular bisector PQ of AX.
∴ XB = AB
Since, C lies on the perpendicular bisector RS of AY.
∴ CY = AC
Thus, AB+BC+CA=XB+CY=XY
Again, ∠BAX=∠AXB [∵ in ΔAXB, AB = XB]....(i)
Also, ∠ABC=∠BAX+∠AXB [∵∠ABC is an exterior angle of ΔAXB]
= ∠AXB+∠AXB [from Eq. (i)]
= 2∠AXB=∠LXY [∵ AX is a bisector of ∠LXB]
Also, ∠CAY=∠AYC [∵∈ΔAYC, AC = CY]
∴∠ACB=∠CAY+∠AYC [∵∠ACB is an exterior angle of ΔAYC]
= ∠CAY+∠CAY
= 2∠CAY=∠MYX [∵ AY is a bisector of ∠MYX]
Thus, our construction is justified.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The difference between the sides at right angles in a right - angled triangle is 14 cm . The area of the trangle is 120cm2 . Calculate the perimeter of the triangle.
A68 cmB64 cmC60 cmD58 cmThe area of a right angled triangle is 6 sq . Cm and its perimeter is 12 cm . The length of its hypotenuse is
A6 cmB5 cmC2 cmDData insufficient
Construct a right-angled triangle whose perimeter is equal to 10cm and one acute angle equal to 600.
View SolutionThe difference between the sides at right angles in a right - angled triangle is 14 cm . The area of the trangle is 120cm2 . Calculate the perimeter of the triangle.
View SolutionIf the difference between the two sides of a right-angled triangle is 2 cm and the area of the triangle is 24cm2 , find the perimeter of the triangle.
View SolutionIf triangle ABC is similar to triangle PQR , Perimeter of triangle ABC = 30 cm , Perimeter of triangle = 45 cm , PR = 9 cm then find AC.
View SolutionIf the difference between the sides of a right angled triangle is 3 cm and its area is 54 cm2, find its perimeter.
View SolutionIt the difference between the sides of right angles triangle is 3 cm and its area is 54 cm2. Find its perimeter.
View Solution
