If a square ABCD is inscribed in a circle of radius 'r' and AB = 4 cm, then the value of r is :
2 cm
cm
4 cm
cm
The correct Answer is:B
To find the radius r of the circle in which the square ABCD is inscribed, follow these steps:
Step 1: Understand the relationship between the square and the circle
A square inscribed in a circle means that all four corners of the square touch the circle. The distance from the center of the circle to any vertex of the square is the radius r.
Step 2: Identify the side length of the square
Given that the side length AB of the square is 4 cm, we can denote this side length as s:
s=4 cm
Step 3: Relate the side length of the square to the radius of the circle
The radius r of the circle can be calculated using the formula that relates the side length of the square to the radius of the circumscribed circle:
r=s√22
This formula arises because the diagonal of the square is equal to the diameter of the circle, and the diagonal d of a square can be calculated as:
d=s√2
Since the diameter D of the circle is twice the radius, we have:
D=2r=s√2
Thus, rearranging gives:
r=s√22
Step 4: Substitute the value of s
Now, substitute s=4 cm into the formula:
r=4√22
Step 5: Simplify the expression
Simplifying the expression gives:
r=2√2 cm
Final Answer
Thus, the value of r is:
r=2√2 cm
---
A square inscribed in a circle means that all four corners of the square touch the circle. The distance from the center of the circle to any vertex of the square is the radius r.
Given that the side length AB of the square is 4 cm, we can denote this side length as s:
s=4 cm
The radius r of the circle can be calculated using the formula that relates the side length of the square to the radius of the circumscribed circle:
r=s√22
This formula arises because the diagonal of the square is equal to the diameter of the circle, and the diagonal d of a square can be calculated as:
d=s√2
Since the diameter D of the circle is twice the radius, we have:
D=2r=s√2
Thus, rearranging gives:
r=s√22
Now, substitute s=4 cm into the formula:
r=4√22
Simplifying the expression gives:
r=2√2 cm
Thus, the value of r is:
r=2√2 cm
Topper's Solved these Questions
- AREAS RELATED TO CIRCLES BOOK - EDUCART PUBLICATIONCHAPTER - AREAS RELATED TO CIRCLES EXERCISE - OBJECTIVE TYPE QUESTION (FILL IN THE BLANKS)
8 Videos
- AREAS RELATED TO CIRCLES BOOK - EDUCART PUBLICATIONCHAPTER - AREAS RELATED TO CIRCLES EXERCISE - OBJECTIVE TYPE QUESTION (VERY SHORT QUESTIONS)
12 Videos
- ARITHMETIC PROGRESSIONSBOOK - EDUCART PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - LONG ANSWER TYPE QUESTIONS
44 Videos
Similar Questions
Knowledge Check
If a square is inscribed in a circle of radius 7 cm, then find the area of the square (in cm2).
A49B98C196D392If a square is inscribed in a circle of radius 7 cm, then find the area of the square (in cm2).
A49B98C196D392The area of the square inscribed in a circle of radius 8 cm is
A256 sq. cmB250 sq. cmC128sq. CmD125 sq. cm
Q. 46 A square ABCD is inscribed in a circle and AB = 4 cm, then radius of the circle is:(A) 2 cm(B) 2/2 cm(C) 4 cm(D) 412 cm
View Solution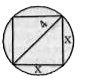
A square of side x is inscribed in a circle of radius 4 cm. Then x is
View SolutionFind the area of a square inscribed in a circle of radius 5 cm.
View SolutionThe square ABCD is inscribed in a circle of radius 1 unit. ABP is a straight line, PC is tangent to the circle. The length of PD is
View SolutionFind the area of a square inscribed in a circle of radius 4 cm.
View Solution
