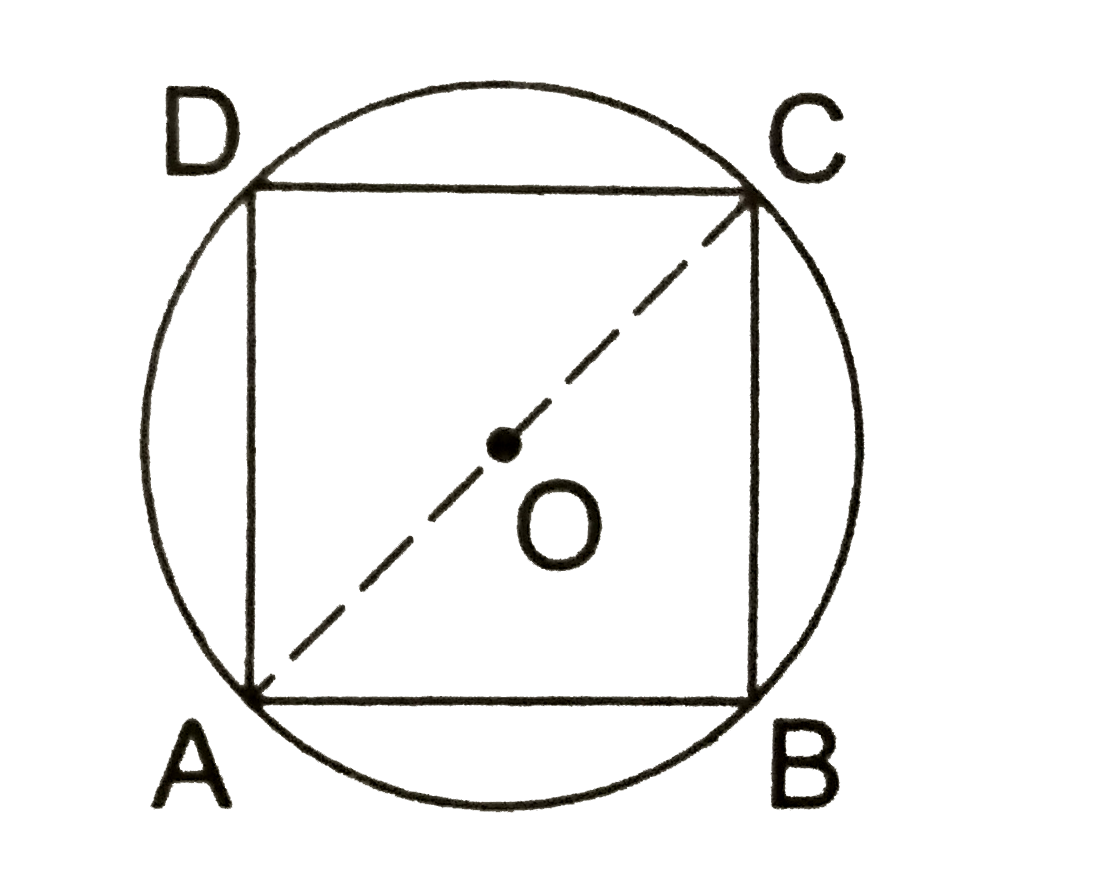
A square ABCD is inscribed in a circle of radius $r$ . Find the area of the square.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $(2 r^{2}$ sq units

Let $O$ be the centre of the given circle and let ABCD be the square inscribed in it.
So, diag. $A C = 2 r$
ar(squareABCD) $= \frac{1}{2} \times {(diagonal)}^{2} = {\frac{1}{2} \times {(2 r)}^{2}}$ sq units $= (2 r^{2})$ sq units

|

Updated on:21/07/2023

Class 10 MATHS AREAS RELATED TO CIRCLES

Topper's Solved these Questions

BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - Multiple Choice Questions (Mcq)
26videos
AREA OF CIRCLE, SECTOR AND SEGMENT
BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - Test Yourself
19videos
AREA OF CIRCLE, SECTOR AND SEGMENT
BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - EXERCISE
1videos
AREA OF CIRCLE, SECTOR AND SEGMENT
BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)
30videos
ARITHMETIC PROGRESSION

Similar Questions

Knowledge Check

Question 1 - Select One
If a square is inscribed in a circle of radius 7 cm, then find the area of the square (in $c m^{2}$ ).
A49
B98
C196
D392
Question 2 - Select One
If a square is inscribed in a circle of radius 7 cm, then find the area of the square (in $c m^{2}$ ).
A49
B98
C196
D392
Question 3 - Select One
The area of the largest possible square inscribed in a circle of unit radius ( in square unit ) is :
A2
B $π$
C $(2 \sqrt{2}) π$
D $(4 \sqrt{2}) π$

RS AGGARWAL-AREA OF CIRCLE, SECTOR AND SEGMENT -Exercise 16B

Home
Ask Doubt
Profile