If a triangle is inscribed in an ellipse and two of its sides are parallel to the given straight lines, then prove that the third side touches the fixed ellipse.
Step by step video solution for If a triangle is inscribed in an ellipse and two of its sides are parallel to the given straight lines, then prove that the third side touches the fixed ellipse. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A triangle is inscribed in the hyperbola xy=c2 and two of its sides are parallel to y=m1xandy=m2x. Prove that the third side touches the hyperbola 4m1m2xy=c2(m1+m2)2.
View SolutionFind the length of the third side of the triangle.
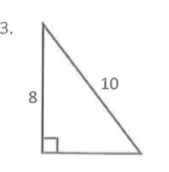
View SolutionFind the length of the third side of the triangle.
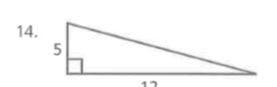
View SolutionAn equilateral triangle is inscribed in an ellipse whose equation is x2+4y2=4 If one vertex of the triangle is (0,1) then the length of each side is
View SolutionAn equilateral triangle is inscribed in a circle of radius 6cm. Find its side.
View SolutionProve that any two sides of a triangle are together greater than twice the median drawn to the third side.
View SolutionIf two sides of a triangle are ˆi+2ˆjandˆi+ˆk, then find the length of the third side.
View SolutionIf a triangle is inscribed in a circle, then prove that the product of any two sides of the triangle is equal to the product of the diameter and the perpendicular distance of the thrid side from the opposite vertex.
View SolutionAn equilateral triangle is inscribed in the parabola y2=8x with one of its vertices is the vertex of the parabola. Then, the length or the side or that triangle is
View SolutionTheorem 6.2 : If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
View Solution
