If a vertex, the circumcenter, and the centroid of a triangle are (0, 0), (3,4), and (6, 8), respectively, then the triangle must be (a) a right-angled triangle (b) an equilateral triangle (c) an isosceles triangle (d) a right-angled isosceles triangleSolution in Bengali
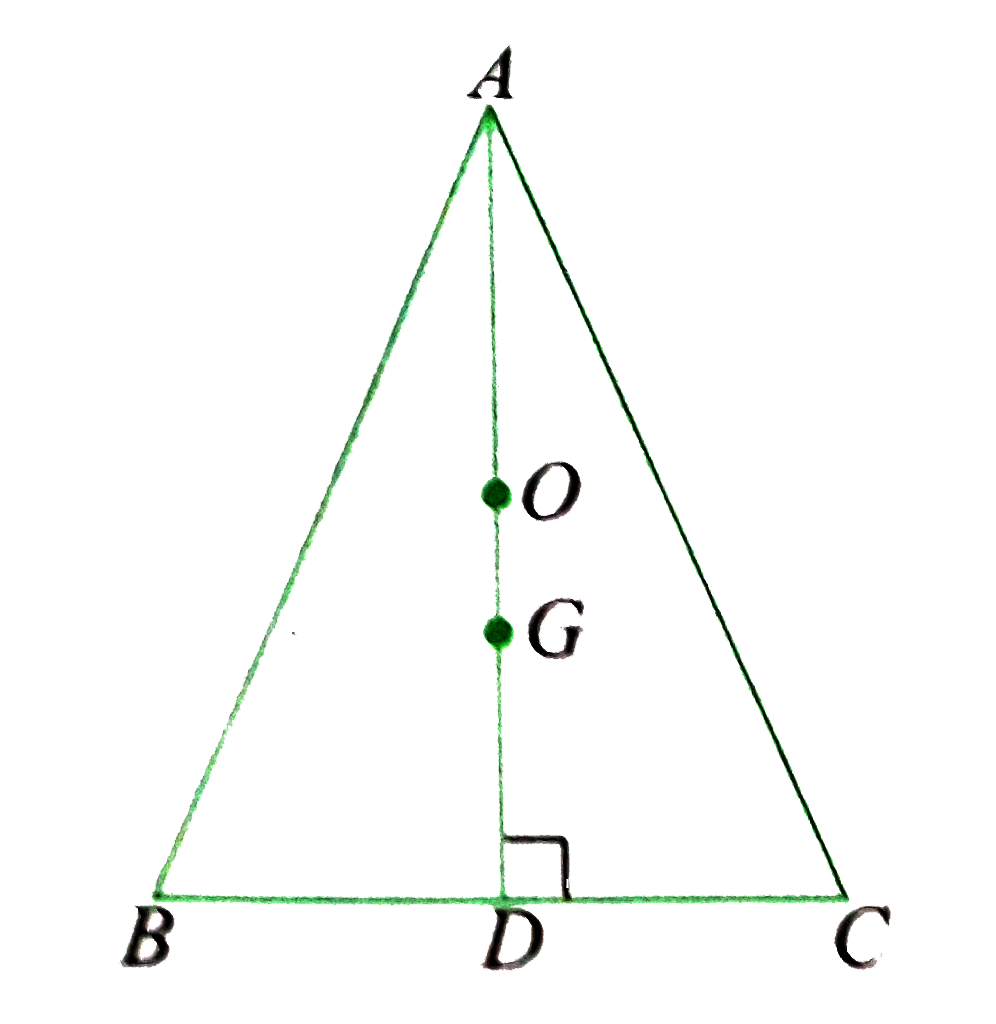
We have vertex A(0,0) circumcentre O(3,4) and centroid G(6,8). Point O lies on the perpendicular bisector (OD) of side BC and point G lies on the median AD.
Now, A O and G are collinear. So median AD and perpendicular bisector (OD) of BC coincide. Thus, AD is the perpendicular bisector of BC. Therefore, triangle ABC is isosceles.
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.34
1 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.35
1 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.32
1 Videos
- COORDINATE SYSTEMBOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
If the circumcenter of an acute-angled triangle lies at the origin and the centroid is the middle point of the line joining the points (a2+1,a2+1) and (2a,−2a), then find the orthocentre.
View SolutionOrthocenter and circumcenter of a ΔABC are (a,b)and(c,d) , respectively. If the coordinates of the vertex A are (x1,y1), then find the coordinates of the middle point of BC.
View SolutionFind the orthocentre of the triangle whose vertices are (0,0),(3,0), and (0,4).
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionIn a triangle a=2b and A=3B .Mention which of the following is true? A.) The triangle is equilateral B.) The triangle is isosceles C.) The triangle is right angled D.) The existence of such a triangle is not possible
View SolutionIf a vertex, the circumcenter, and the centroid of a triangle are (0, 0), (3,4), and (6, 8), respectively, then the triangle must be (a) a right-angled triangle (b) an equilateral triangle (c) an isosceles triangle (d) a right-angled isosceles triangle
View SolutionIf all the vertices of a triangle have integral coordinates, then the triangle may be (a) right-angle(b) equilateral (c) isosceles(d) none of these
View SolutionIncentre of a triangle lies in the interior of: (A) an isosceles triangle only (B) a right angled triangle only (C) any equilateral triangle only (D) any triangle
View SolutionIn any triangle ABC if 2cos B=(a)/(c), then the triangle is(A) Right angled (C) Isosceles (B) Equilateral (D) None of these
View SolutionIf one angle of a triangle is equal to the sum of the other two angles, then the triangle is an isosceles triangle (b) an obtuse triangle an equilateral triangle (d) a right triangle
View SolutionIf A = {Equilateral triangles }, B = {Right angled triangles } and C = { Isosceles trian - gles } , then
View SolutionIn triangle ABC,R(b+c)=a√bc,where R is the circumradius of the triangle. Then the triangle is
View SolutionIf a vertex, the circumcenter, and the centroid of a triangle are (0, 0), (3,4), and (6, 8), respectively, then the triangle must be (a) a right-angled triangle (b) an equilateral triangle (c) an isosceles triangle (d) a right-angled isosceles triangle
View SolutionIf all the vertices of a triangle have integral coordinates, then the triangle may be (a) right-angle (b) equilateral (c) isosceles (d) none of these
View SolutionIf one angle of a triangle is equal to the sum of the other two angles, then the triangle is (a) an isosceles triangle (b) an obtuse triangle (c) an equilateral triangle (d) a right triangle
View Solution
