If a vertex, the circumcenter, and the centroid of a triangle are (0, 0), (3,4), and (6, 8), respectively, then the triangle must be (a) a right-angled triangle (b) an equilateral triangle (c) an isosceles triangle (d) a right-angled isosceles triangle
To determine the type of triangle given the vertex, circumcenter, and centroid, we will follow these steps:
Step 1: Identify the points
The points given are:
- Vertex A(0,0)
- Circumcenter O(3,4)
- Centroid G(6,8)
Step 2: Check for collinearity
To check if the three points are collinear, we can calculate the area of the triangle formed by these points. If the area is zero, then the points are collinear.
The formula for the area of a triangle given three vertices (x1,y1), (x2,y2), and (x3,y3) is:
Area=12|x1(y2−y3)+x2(y3−y1)+x3(y1−y2)|
Substituting the points:
- (x1,y1)=(0,0)
- (x2,y2)=(3,4)
- (x3,y3)=(6,8)
Calculating the area:
Area=12|0(4−8)+3(8−0)+6(0−4)|
=12|0+24−24|=12|0|=0
Since the area is zero, the points are collinear.
Step 3: Analyze the implications of collinearity
Since the circumcenter and centroid are collinear with the vertex, we can conclude that the triangle must be isosceles.
In an isosceles triangle, the centroid lies on the median, and the circumcenter lies on the perpendicular bisector of the base. Given that all three points are collinear, this means the triangle can only be isosceles or equilateral.
Step 4: Determine the type of triangle
However, for the triangle to be equilateral, all three vertices must be collinear, which is not the case here. Thus, we conclude that the triangle is isosceles.
Conclusion
The triangle must be an isosceles triangle.
The points given are:
- Vertex A(0,0)
- Circumcenter O(3,4)
- Centroid G(6,8)
To check if the three points are collinear, we can calculate the area of the triangle formed by these points. If the area is zero, then the points are collinear.
- (x1,y1)=(0,0)
- (x2,y2)=(3,4)
- (x3,y3)=(6,8)
Since the circumcenter and centroid are collinear with the vertex, we can conclude that the triangle must be isosceles.
However, for the triangle to be equilateral, all three vertices must be collinear, which is not the case here. Thus, we conclude that the triangle is isosceles.
The triangle must be an isosceles triangle.
Topper's Solved these Questions
Similar Questions
A triangle whose all sides are equal is called
View SolutionCan an acute-angled triangled be a. and equilateral, b. an isosceles, and c. a scalene triangle ?
View SolutionDetermine the measure of each of the equal angles of a right-angled isosceles triangle.
View SolutionIf the sides of a triangle are 3 cm, 4 cm and 6 cm long, determine whether the triangle is a right-angle triangle.
View SolutionA triangle whose two sides are equal is called (a) an acute triangle (b) a scalene triangle (c) an isosceles triangle (d) an equilateral triangle
View SolutionIf the sides of a triangle are 3 cm, 4 cm and 6 cm long, determine whether the triangle is right-angled triangle.
View SolutionIn figure ABC is an isosceles triangle , right angled at C . Therefore
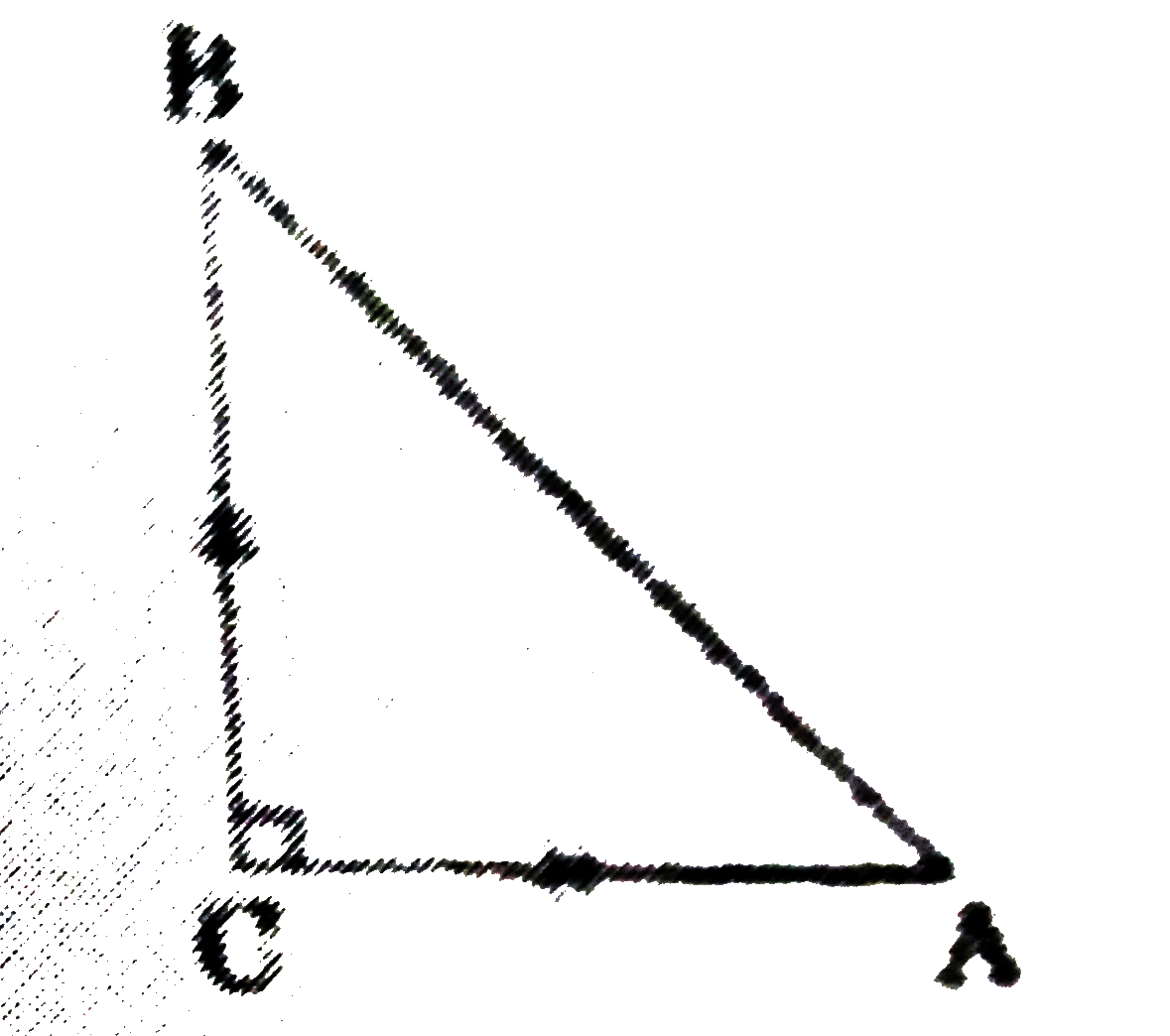
View SolutionIf one angle of a triangle is equal to the sum of the other two angles, then the triangle is (a) an isosceles triangle (b) an obtuse triangle (c) an equilateral triangle (d) a right triangle
View SolutionIdentify the following triangles as equilateral, isosceles, scalene, acute-angled, right-angled, and obtuse-angled triangles.
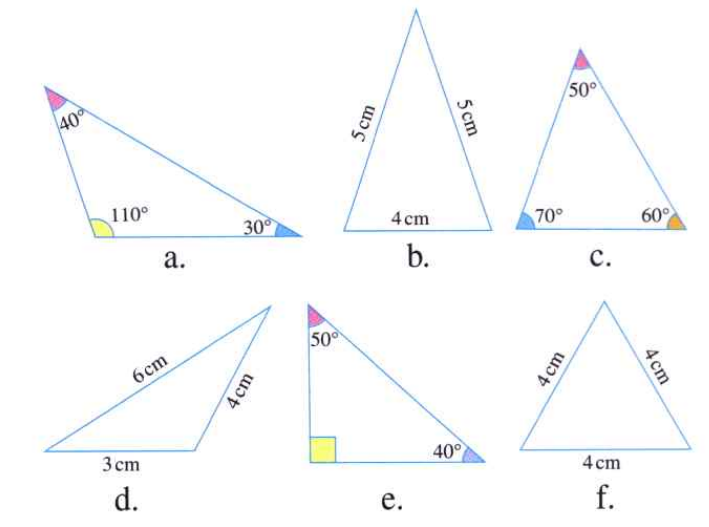
View SolutionA triangle whose two sides are equal is known as
View Solution
