If $A_{1} B_{2}$ and $A_{2} B_{2}$ are two focal chords of the parabola $y^{2} = 4 a x$ then the chords $A_{1} A_{2}$ and $B_{1} B_{2}$ intersect on

A

directrix

B

axis

C

T.V.

D

none

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:A

To solve the problem, we need to find the intersection point of the chords $A_{1} A_{2}$ and $B_{1} B_{2}$ for the parabola given by the equation $y^{2} = 4 a x$ .
1. Identify Points on the Parabola:
- The points $A_{1}$ and $A_{2}$ are focal chords of the parabola. For a parabola $y^{2} = 4 a x$ , the coordinates of points on the parabola can be expressed in terms of the parameter $t$ .
- Let $A_{1} = (a t_{1}^{2}, 2 a t_{1})$ and $A_{2} = (a t_{2}^{2}, 2 a t_{2})$ .
- The corresponding points $B_{1}$ and $B_{2}$ on the parabola can be calculated using the properties of focal chords:
- $B_{1} = (\frac{a}{t_{1}^{2}}, - \frac{2 a}{t_{1}})$
- $B_{2} = (\frac{a}{t_{2}^{2}}, - \frac{2 a}{t_{2}})$
2. Equation of Line $A_{1} A_{2}$ :
- The slope of the line joining points $A_{1}$ and $A_{2}$ is given by:
$slope = \frac{2 a t_{2} - 2 a t_{1}}{a t_{2}^{2} - a t_{1}^{2}} = \frac{2 a (t_{2} - t_{1})}{a (t_{2}^{2} - t_{1}^{2})} = \frac{2 (t_{2} - t_{1})}{t_{2}^{2} - t_{1}^{2}}$
- The equation of the line $A_{1} A_{2}$ can be written as:
$y - 2 a t_{1} = \frac{2 (t_{2} - t_{1})}{t_{2}^{2} - t_{1}^{2}} (x - a t_{1}^{2})$
3. Equation of Line $B_{1} B_{2}$ :
- Similarly, the slope of the line joining points $B_{1}$ and $B_{2}$ is:
$slope = \frac{- \frac{2 a}{t_{2}} + \frac{2 a}{t_{1}}}{\frac{a}{t_{2}^{2}} - \frac{a}{t_{1}^{2}}} = \frac{- 2 a (\frac{1}{t_{2}} - \frac{1}{t_{1}})}{a (\frac{1}{t_{2}^{2}} - \frac{1}{t_{1}^{2}})}$
- The equation of the line $B_{1} B_{2}$ can be written as:
$y + \frac{2 a}{t_{1}} = \frac{- 2 (\frac{1}{t_{2}} - \frac{1}{t_{1}})}{\frac{1}{t_{2}^{2}} - \frac{1}{t_{1}^{2}}} (x - \frac{a}{t_{1}^{2}})$
4. Finding Intersection Point:
- To find the intersection point of the two lines, we set the equations equal to each other and solve for $x$ and $y$ .
- After simplifying, we will find that the intersection point lies on the directrix of the parabola, which is given by the equation $x + a = 0$ .
5. Conclusion:
- Therefore, the intersection of the chords $A_{1} A_{2}$ and $B_{1} B_{2}$ lies on the directrix of the parabola, which is the line $x + a = 0$ .

Updated on:7/8/2024

|

Class 12 MATHS PARABOLA

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two AMs. $A_{1}$ and $A_{2}$ , two GMs. $G_{1}$ and $G_{2}$ and two HMs. $H_{1}$ and $H_{2}$ are inserted between any two numbers. Then find the arithmetic mean between $H_{1}$ and $H_{2}$ in terms of $A_{1}, A_{2}, G_{1}, G_{2}$ .
A $\frac{A_{1} + A_{2}}{2 G_{1} G_{2}}$
B $\frac{A_{1} - A_{2}}{2 G_{1} G_{2}}$
C $\frac{A_{1} + A_{2}}{2 + G_{1} G_{2}}$
D $\frac{G_{1} + G_{2}}{2 A_{1} A_{2}}$
The capacitance of the capacitors of plate areas $A_{1}$ and $A_{2} (A_{1} < A_{2})$ at a distance d is

A $\frac{ε_{0} A_{1}}{d}$
B $\frac{ε_{0} A_{2}}{d}$
C $\frac{ε_{0} (A_{1} + A_{2})}{2 d}$
D $\frac{ε_{0} \sqrt{A_{1} A_{2}}}{d}$
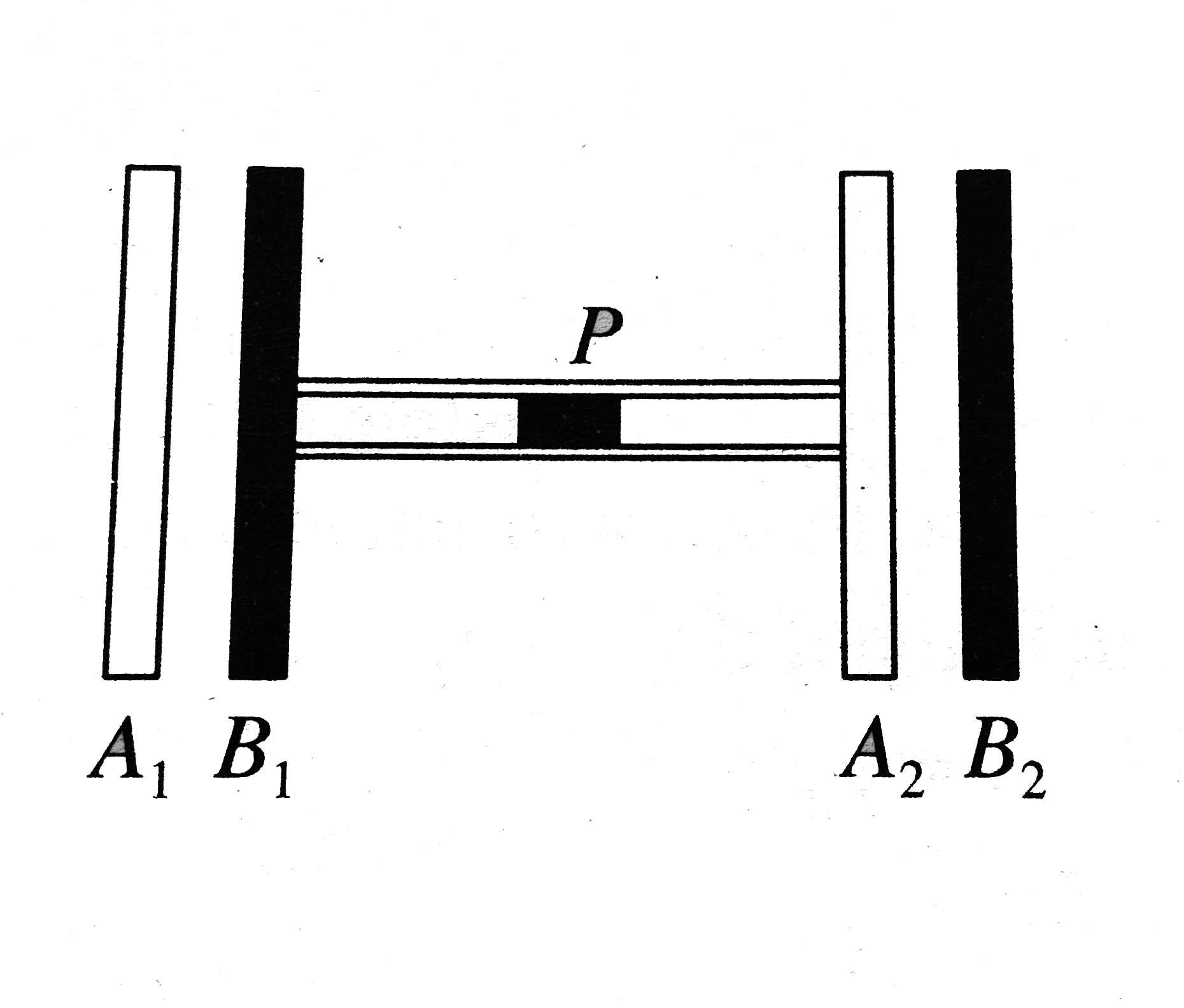
Two plates identical in size, one of black and rough surface $(B_{1})$ and the other smooth and polished $(A_{2})$ are in terconnected by a thin horizontal pipe with a mercury pellet at the centre. Two more plates $A_{1}$ (identical to $A_{2}$ ) and $B_{2}$ (identical $B_{1}$ ) are heated to the same temperature and placed closed to the plates $B_{1}$ , and $A_{2}$ shown in Fig. The mercury pellet
Amoves to the right
Bmoves to the left
Cremains stationary
Dstarts oscillating left and right

ML KHANNA-THE PARABOLA -Problem Set (2) (MULTIPLE CHOICE QUESTIONS)

Home
Ask Doubt
Profile