Let L be the line created by rotating the tangent line to the parabola y=x2 at the point (1,1), about A by an angle (−π4). Let B be the other intersection of line L with y=x2. If the area inclosed by the L and the parabola is (a1a2) where a1anda2 are co prime numbers, find(a1+a2)
Step by step video & image solution for Let L be the line created by rotating the tangent line to the parabola y=x^2 at the point (1,1), about A by an angle (-pi/4). Let B be the other intersection of line L with y=x^2. If the area inclosed by the L and the parabola is (a_1/a_2) where a_1 and a_2 are co prime numbers, find(a_1+a_2) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Let the circle x2+y2=4 divide the area bounded by tangent and normal at (1,√3) and x-axis in A1andA2. Then A1A2 equals to
View SolutionIf A1 is the area of the parabola y2=4ax lying between vertex and the latusrectum and A2 is the area between the latusrectum and the double ordinate x=2a, then A1A2 is equal to
View Solution
Knowledge Check
If A1B2 and A2B2 are two focal chords of the parabola y2=4ax then the chords A1A2 and B1B2 intersect on
AdirectrixBaxisCT.V.DnoneThe capacitance of the capacitors of plate areas A1 and A2(A1<A2) at a distance d is
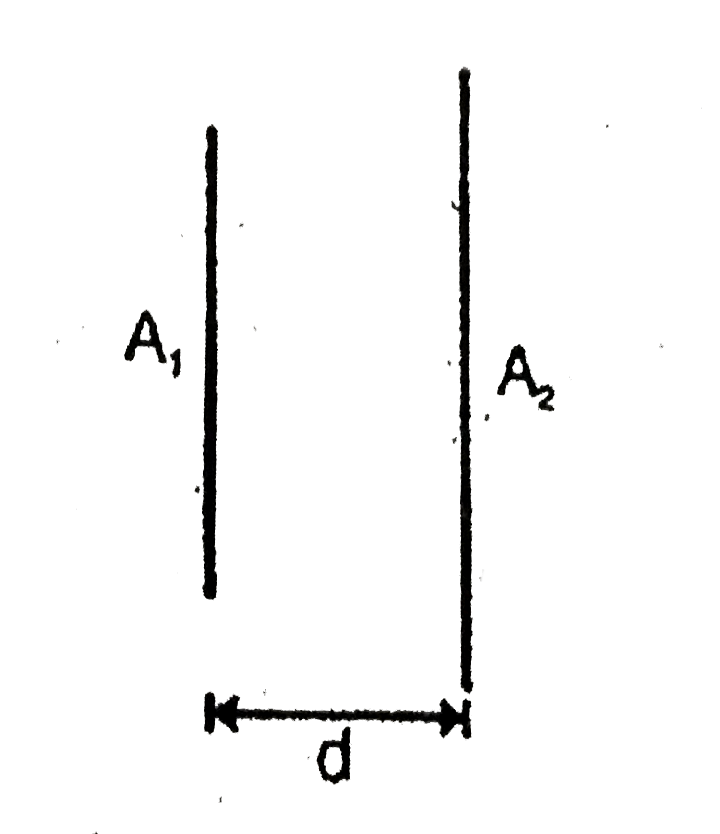 Aε0A1dBε0A2dCε0(A1+A2)2dDε0√A1A2d
Aε0A1dBε0A2dCε0(A1+A2)2dDε0√A1A2d
If the area of the circle is A1 and the area of the regular pentagon inscribed in the circle is A2, then find the ratio A1A2.
View SolutionIf the area of the circle is A1 and the area of the regular pentagon inscribed in the circle is A2, then find the ratio A1A2.
View SolutionThe capacitance of the capacitors of plate areas A1 and A2(A1<A2) at a distance d is

View SolutionLet A be the set of 4-digit numbers a1a2a3a4 where a1>a2>a3>a4, then n(A) is equal to
View SolutionLet A be the set of 4-digit numbers a1a2a3a4 where a1>a2>a3>a4, then n(A) is equal to
View SolutionLet L1andL2 be two lines intersecting at P If A1,B1,C1 are points on L1,A2,B2,C2,D2,E2 are points on L2 and if none of these coincides with P, then the number of triangles formed by these 8 points is
View Solution
