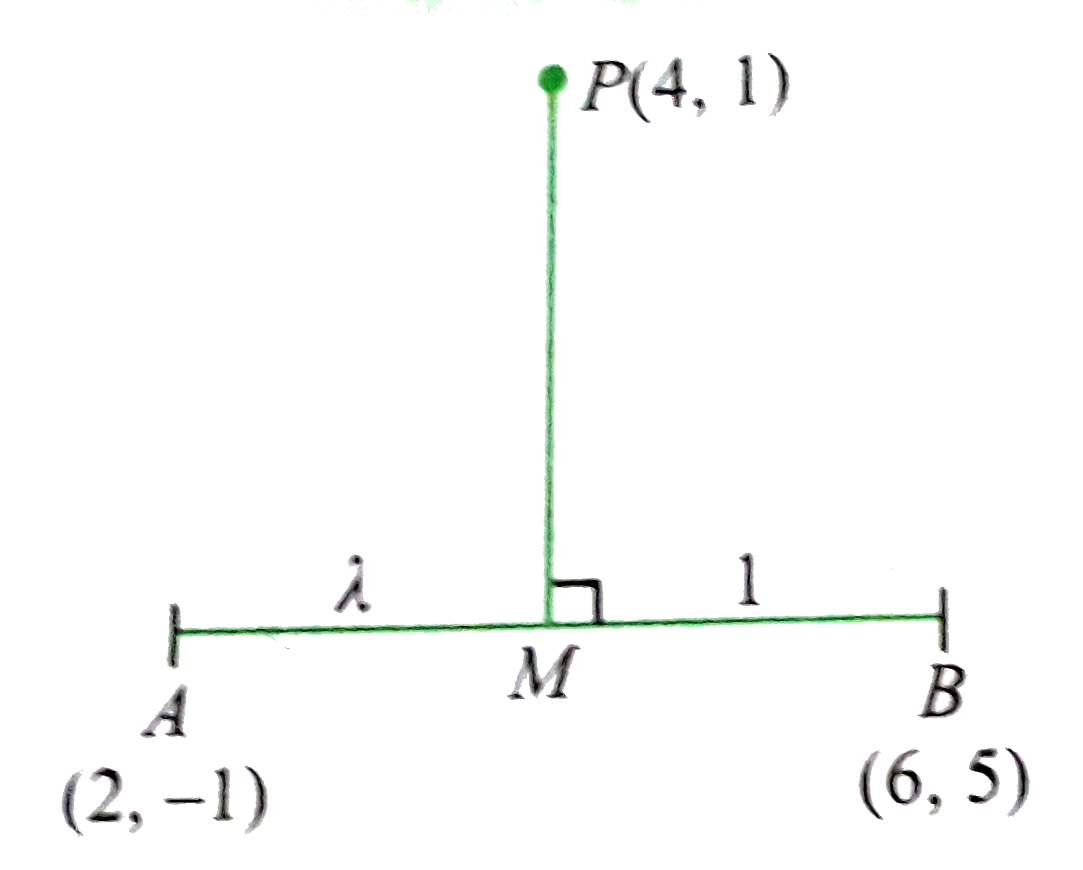
If $A (2, - 1) a n d B (6, 5)$ are two points, then find the ratio in which the food of the perpendicular from $(4, 1)$ to $A B$ divides it.

Video Solution

Text Solution

Verified by Experts

Let $\frac{A M}{M B} = \frac{λ}{1}$
Therefore, the coordinates of M are
$(\frac{6 λ + 2}{λ + 1}, \frac{5 λ - 1}{λ + 1})$
$∴ P M ⊥ A B$
or $⎛ ⎜ ⎝ \frac{\frac{5 λ - 1}{λ + 1} - 1}{\frac{6 λ + 2}{λ + 1} - 4} ⎞ ⎟ ⎠ {\frac{5 - 1 (- 1)}{6 - 2}} = - 1$
or $(\frac{2 λ - 1}{λ + 1}) (\frac{3}{2}) = - 1$
or $6 λ - 3 = 2 - 2 λ$
or $λ = \frac{5}{8}$

|

Updated on:21/07/2023

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If A(1, 2, 3), B(4, 5, 6) are two points, then the foot of the perpendicular from point B to the line joining the origin and point A is
A $(\frac{8}{7}, \frac{16}{7}, \frac{24}{7})$
B $(\frac{16}{7}, \frac{32}{7}, \frac{48}{7})$
C $(\frac{1}{7}, \frac{2}{7}, \frac{3}{7})$
D $(\frac{4}{7}, \frac{8}{7}, \frac{12}{7})$
Question 2 - Select One
Find the ratio in which the point P(x, 2) divides the join of A(12, 5) and B(4, -3).
A5 : 3
B3 : 5
C1 : 3
D3 : 2
Question 3 - Select One
What is the ratio in which point P(1, 2) divides the join of A(-2, 1) and B(7,4)?
A $1 : 2$
B $2 : 1$
C $3 : 4$
D $2 : 3$

CENGAGE-COORDINATE SYSYEM -JEE Main Previous Year

Home
Ask Doubt
Profile