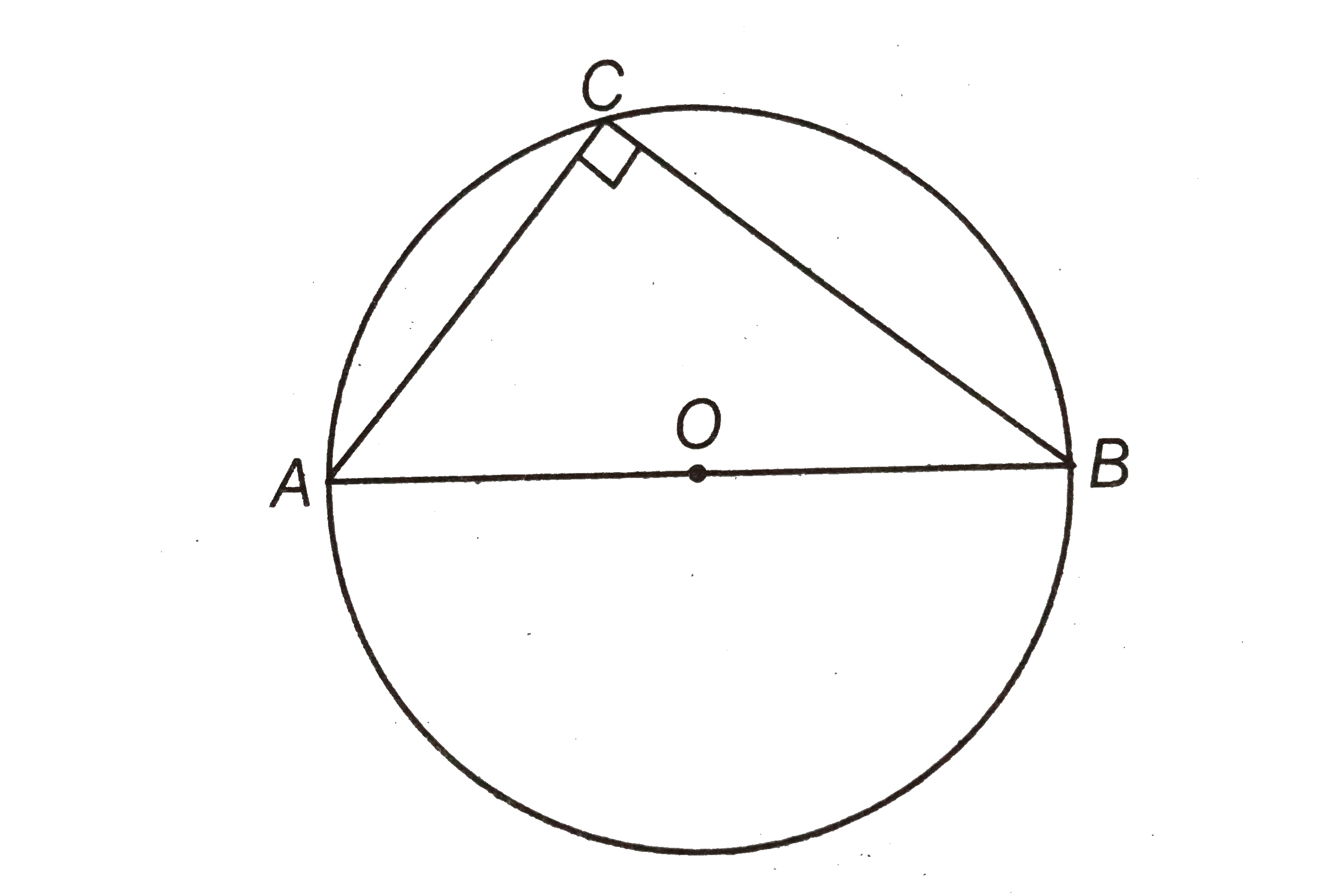
If AOB is a diameter of a circle and C is a point on the circle, then AC2+BC2=AB2.
The correct Answer is:1
Since, any diameter of the circle subtends a right angle to any point on the circle.
If AOB is a diameter of a circle and C is a point on the circle, then ΔACB is right angled atC.
In right angled ΔACB, [use Pythagoras theorem]
AC2+BC2=AB2
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.4
2 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles
34 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
Knowledge Check
If AOB is a diameter of the circle and AC=BC, then ∠CAB is equal to
A30∘B45∘C60∘D90∘A chord of the circle x2+y2=a2 cuts it at two points A and B such that ∠AOB=π/2, where O is the centre of the circle. If there is a moving point P on this circle, then the locus of the orthocentre of ΔPAB will be a
AparabolaBcircleCstraight lineDnone of these
If Fig , AOB is diameter of a circle with centre O and AC is a tangent to the circle at A . If ∠BOC=130∘ , then find ∠ACO .

View SolutionShow that any angle in a semi-circle is a right angle.
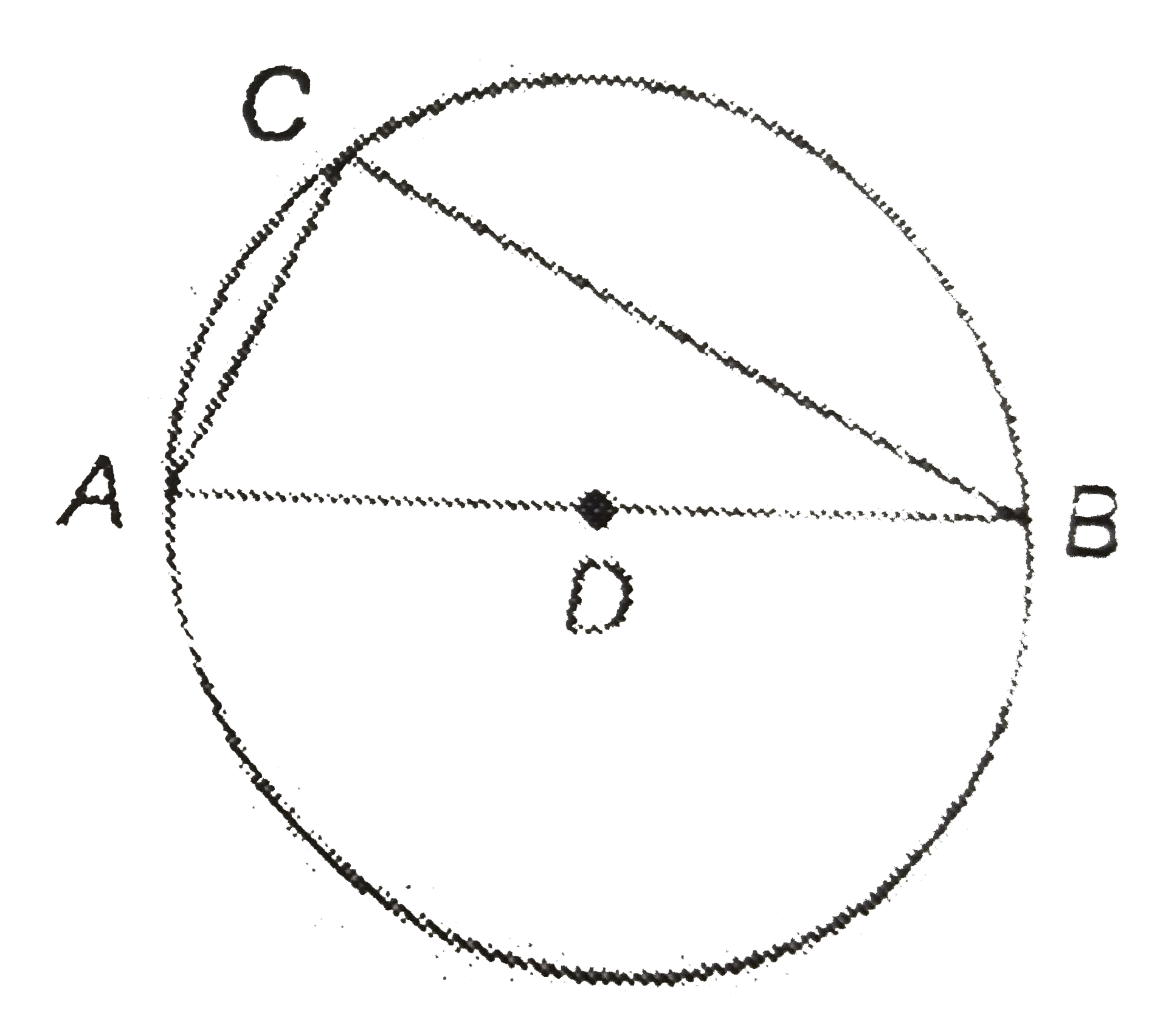
The following arc the steps involved in showing the above result. Arrange them in sequential order.
A) ∴∠ACB=180∘2=90∘
B) The angle subtended by an arc at the center is double of the angle subtended by the same arc at any point on the remaining part of the circle.
c) Let AB be a diameter of a circle with center D and C be any point on the circle. Join AC and BC.
D) ∴∠AD=2×∠ACB
180∘=2∠ACB(∴∠ADB=180∘)
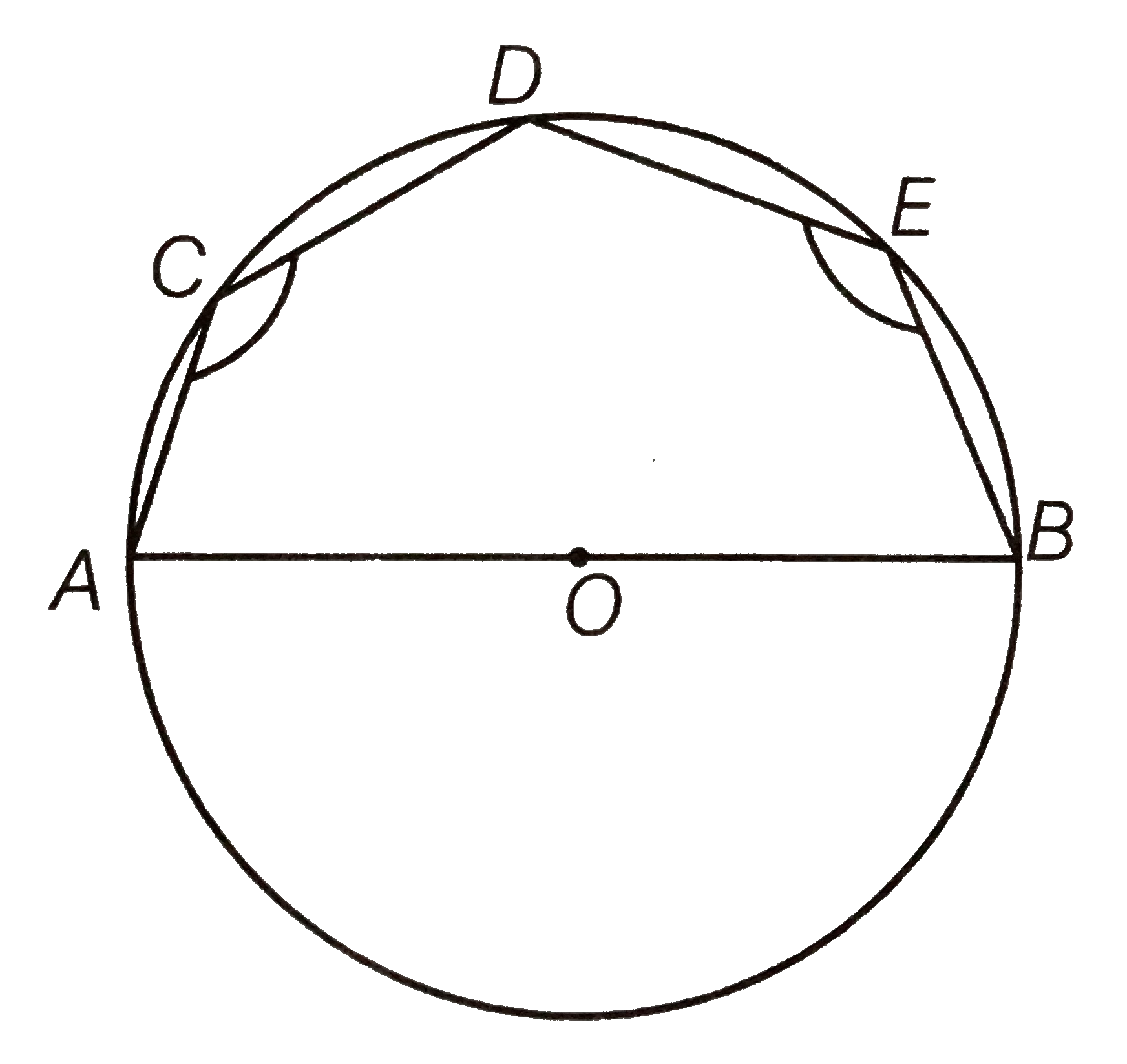
View SolutionIn figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD+∠BED.
View SolutionAB is a chord of a circle with O as centre. C is a point on the circle such that OC is perpendicular to AB and OC intersects AB at P. If PC = 2 cm and AB = 6 cm then the diameter of the circle is
View SolutionAB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tangent at C intersects AB extended at D, then BC=BD.
View SolutionIn the figure, O is the centre of the circle . Seg AB is the diameter at the point C on the circle the tangent CD is drawn. Line BD is a tangent to the circle at point B. Show that seg OD ∣∣ chord AC.
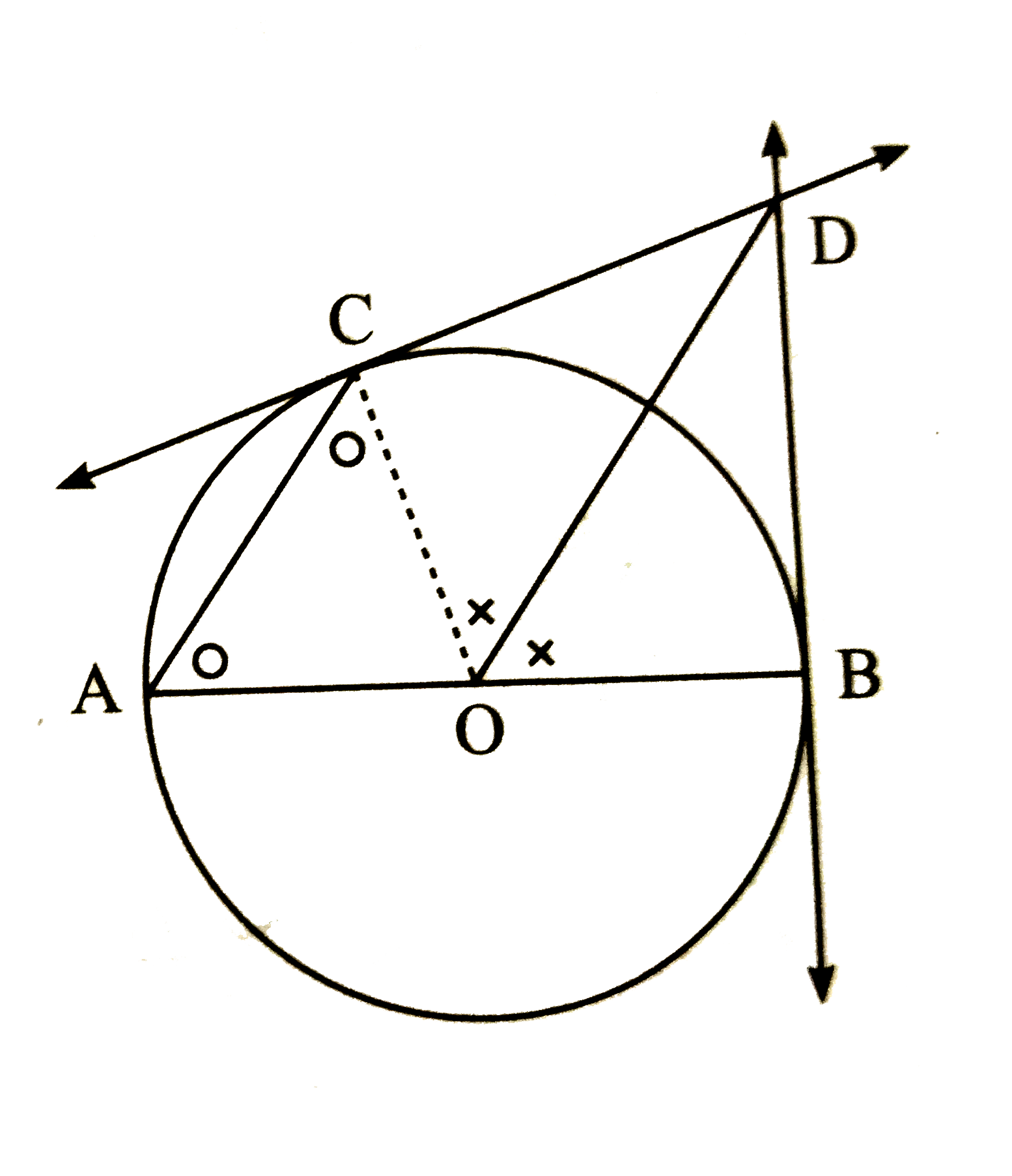
View Solution
