If A={(x,y):y=e−x} and B={(x,y):y=−x}. Then,
A∩B=ϕ
A⊂B
B⊂A
A∩B={(0,1),(0,0)}
The correct Answer is:A
To solve the problem, we need to find the intersection of the two sets A and B.
Step 1: Define the sets
- Set A is defined as A={(x,y):y=e−x}.
- Set B is defined as B={(x,y):y=−x}.
Step 2: Understand the equations
- The equation y=e−x represents an exponential decay function. As x increases, y approaches 0 but never actually reaches it. At x=0, y=1.
- The equation y=−x represents a straight line with a negative slope. It passes through the origin (0,0) and decreases as x increases.
Step 3: Find the intersection
To find the intersection A∩B, we need to set the equations equal to each other:
e−x=−x
Step 4: Analyze the intersection
1. The function e−x is always positive for all real x.
2. The function −x is negative for x>0 and positive for x<0.
Since e−x is positive and −x is negative for x>0, there can be no intersection in that region.
Now, let's check for x<0:
- As x approaches negative infinity, e−x approaches infinity, while −x approaches positive infinity.
- At x=0, e−0=1 and −0=0.
- For x<0, e−x is greater than −x since e−x grows rapidly while −x is linear.
Step 5: Conclusion
Since there are no values of x for which e−x=−x, we conclude that:
A∩B=∅
Final Answer
The intersection of sets A and B is the empty set, denoted as:
A∩B=∅
---
- Set A is defined as A={(x,y):y=e−x}.
- Set B is defined as B={(x,y):y=−x}.
- The equation y=e−x represents an exponential decay function. As x increases, y approaches 0 but never actually reaches it. At x=0, y=1.
- The equation y=−x represents a straight line with a negative slope. It passes through the origin (0,0) and decreases as x increases.
To find the intersection A∩B, we need to set the equations equal to each other:
e−x=−x
1. The function e−x is always positive for all real x.
2. The function −x is negative for x>0 and positive for x<0.
- As x approaches negative infinity, e−x approaches infinity, while −x approaches positive infinity.
- At x=0, e−0=1 and −0=0.
- For x<0, e−x is greater than −x since e−x grows rapidly while −x is linear.
Since there are no values of x for which e−x=−x, we conclude that:
A∩B=∅
The intersection of sets A and B is the empty set, denoted as:
A∩B=∅
Topper's Solved these Questions
- SETS, RELATIONS AND FUNCTIONSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SETS, RELATIONS AND FUNCTIONSEXERCISE - Exercise 1 (TOPICAL PROBLEMS) Relation and Equivalence Relation
10 Videos
- SETS, RELATIONS AND FUNCTIONSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SETS, RELATIONS AND FUNCTIONSEXERCISE - Exercise 1 (TOPICAL PROBLEMS) Types of Mapping
10 Videos
- SEQUENCES AND SERIES BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SEQUENCES AND SERIES EXERCISE - EXERCISE 31
1 Videos
- SOLVED PAPER 2017BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SOLVED PAPER 2017EXERCISE - MCQS
50 Videos
Similar Questions
Knowledge Check
if set A and B are defined as A={(x,y):y=ex,x∈R}
B={(x,y):y=x,x∈R}.thenAB⊂ABA⊂BCA∩B=ϕDA∪Bif set A and B are defined as A={(x,y):y=ex,x∈R}
B={(x,y):y=x,x∈R}.thenAB⊂ABA⊂BCA∩B=ϕDA∪BLet A={(x,y):y=ex,x∈R}B={(x,y),Y=e−x,x∈R}then
AA∩B=ϕBA∩B≠ϕCA∪B=R2Dnone of these
If the sets A and B are defined are defined as A={(x,y):y=ex,x∈R},B={(x,y):y=x,x∈R}then
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
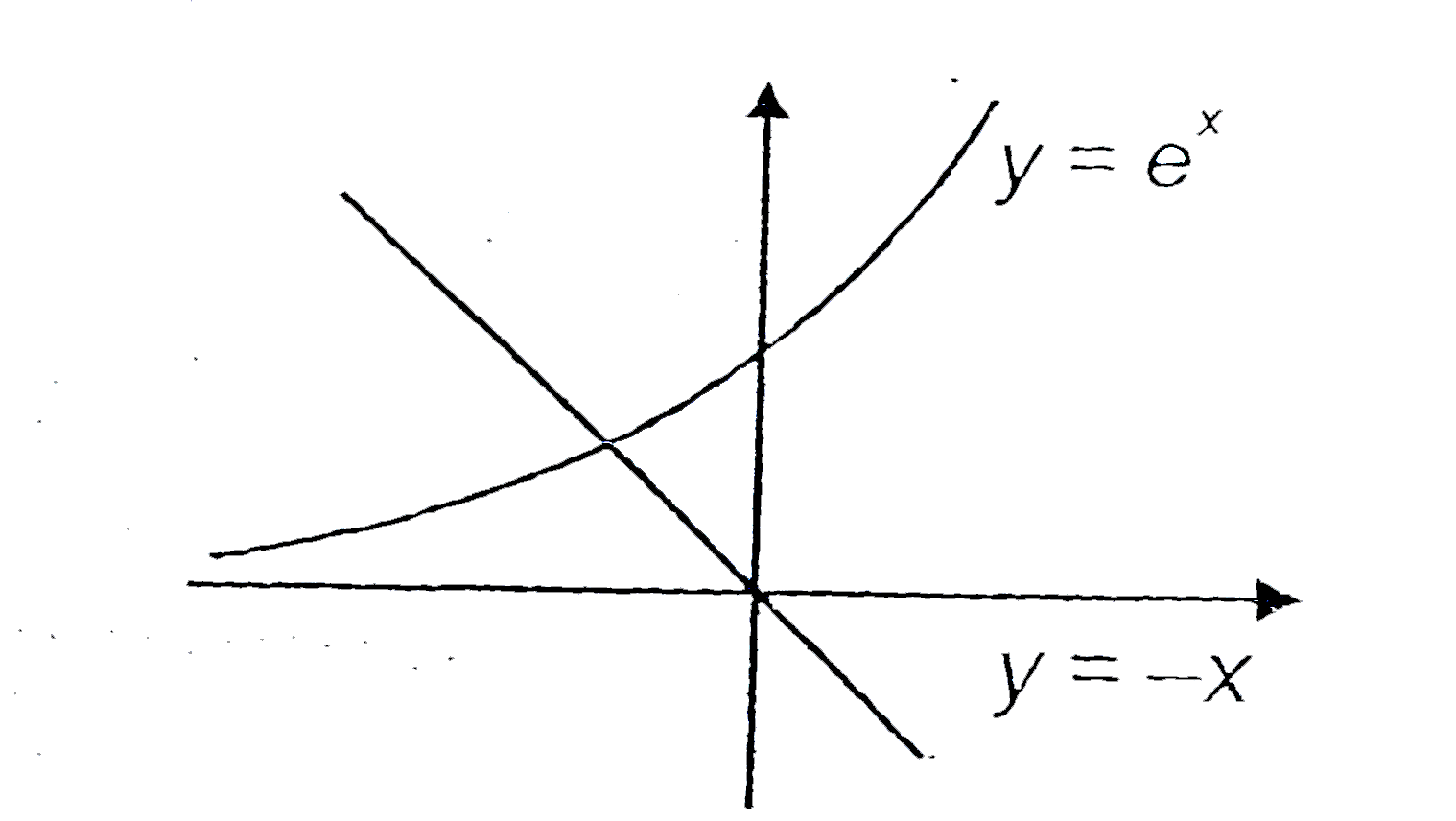
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):x2+y2≤2,x,y∈R}
B={{x,y):y≥x2,x,y∈R}
Then domain of A∩B is
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
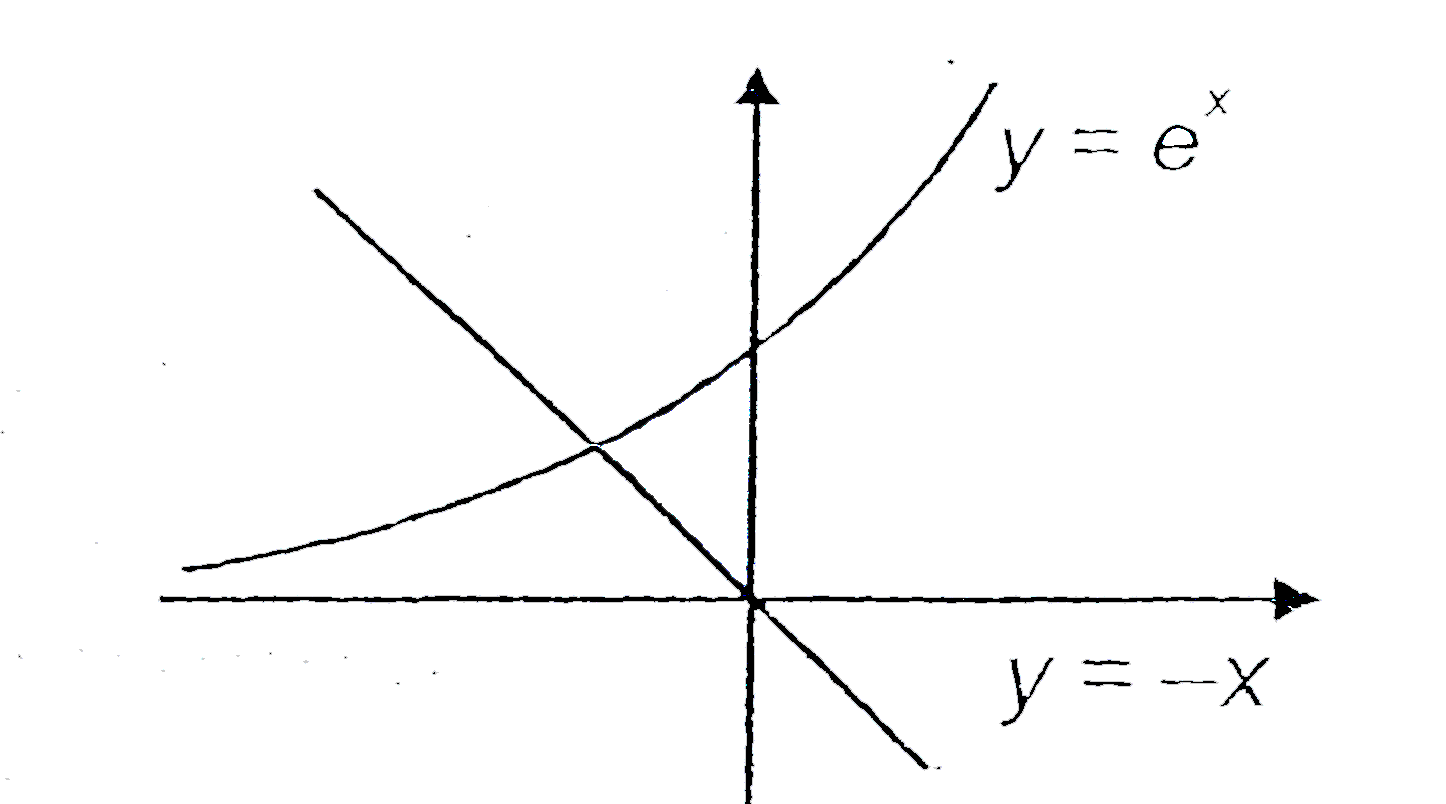
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A:{(x,y):y=√4−x2,x∈[−2,2]}
B={(x,y):y=|x|,x∈R}
Then n(A∩B)
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
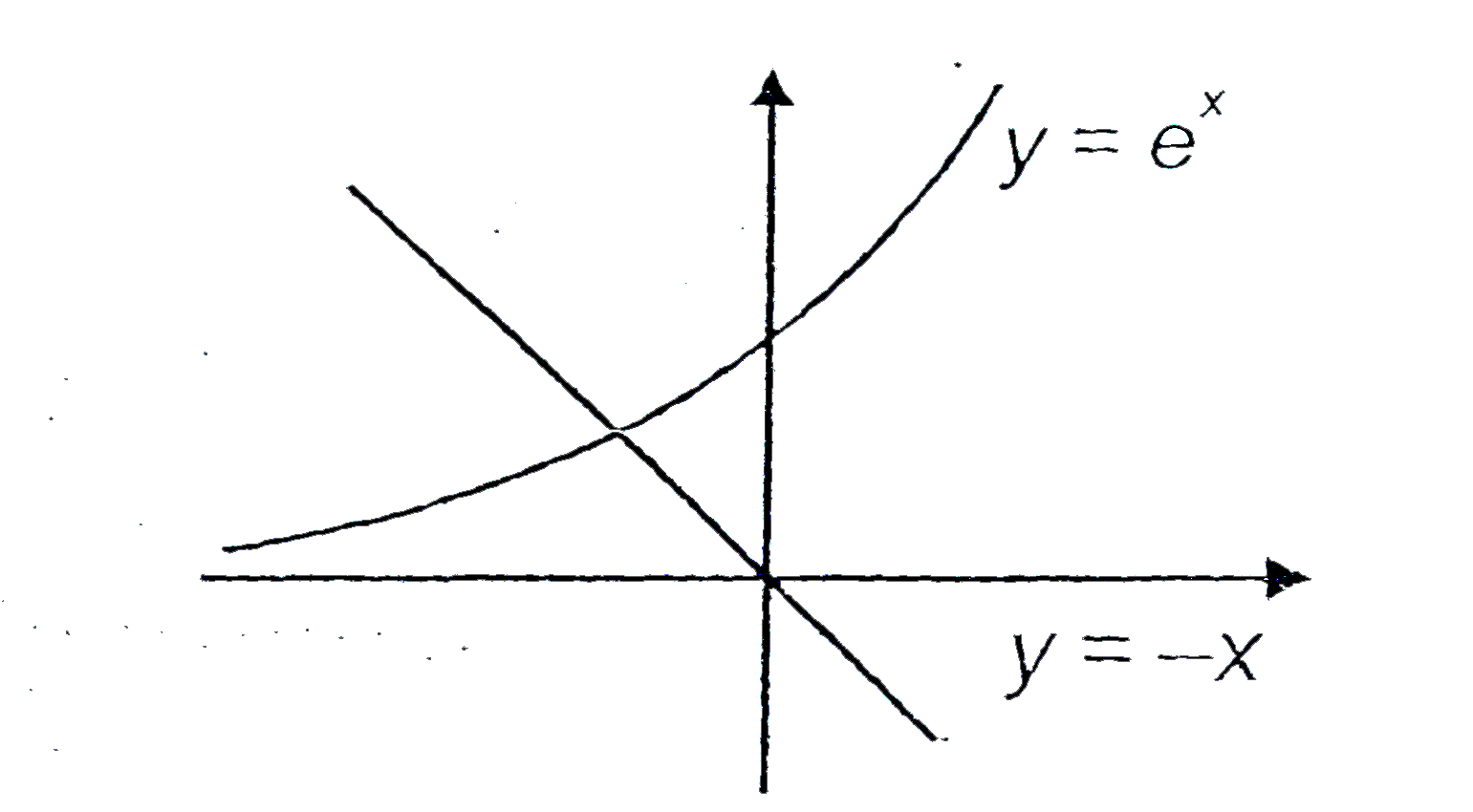
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):y=sinπx,x∈R}
B={(x,y):y=|In|x||,x∈R−{0}}
Then, n(A∩B)
View SolutionIf A={(x,y}: y=3x,y∈R} and B={{x,y}:y=x,x,y∈R} then which of the following is true?
View Solution
