If ¯¯¯E and ¯¯¯F are the complementary events of E and F respectively and if 0<P(F)<1, then
A
P(E/F)+P(¯¯¯E/F)=1
B
P(E/F)+P(E/¯¯¯F)=1
C
P(¯¯¯E/F)+P(E/¯¯¯F)=1
D
P(E/¯¯¯F)+P(¯¯¯E/¯¯¯F)=1
Video Solution
Text Solution
The correct Answer is:A, D
Since E/F and ¯¯¯E/F are complementary events.
∴P(E/F)+P(¯¯¯E/F)=1
Similarly, E/¯¯¯F and ¯¯¯E/¯¯¯F are also complementary events.
∴P(E/¯¯¯F)+P(¯¯¯E/¯¯¯F)=1
|
Topper's Solved these Questions
- PROBABILITY BOOK - OBJECTIVE RD SHARMACHAPTER - PROBABILITY EXERCISE - Section- II (Assertion -Reason Types MCQs)
15 Videos
- PROBABILITY BOOK - OBJECTIVE RD SHARMACHAPTER - PROBABILITY EXERCISE - Section I - Mcqs
94 Videos
- PROBABILITY BOOK - OBJECTIVE RD SHARMACHAPTER - PROBABILITY EXERCISE - Chapter Test
45 Videos
- PERMUTATIONS AND COMBINATIONSBOOK - OBJECTIVE RD SHARMACHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Chapter Test
60 Videos
- QUADRATIC EXPRESSIONS AND EQUATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - QUADRATIC EXPRESSIONS AND EQUATIONS EXERCISE - Chapter Test
50 Videos
Similar Questions
Knowledge Check
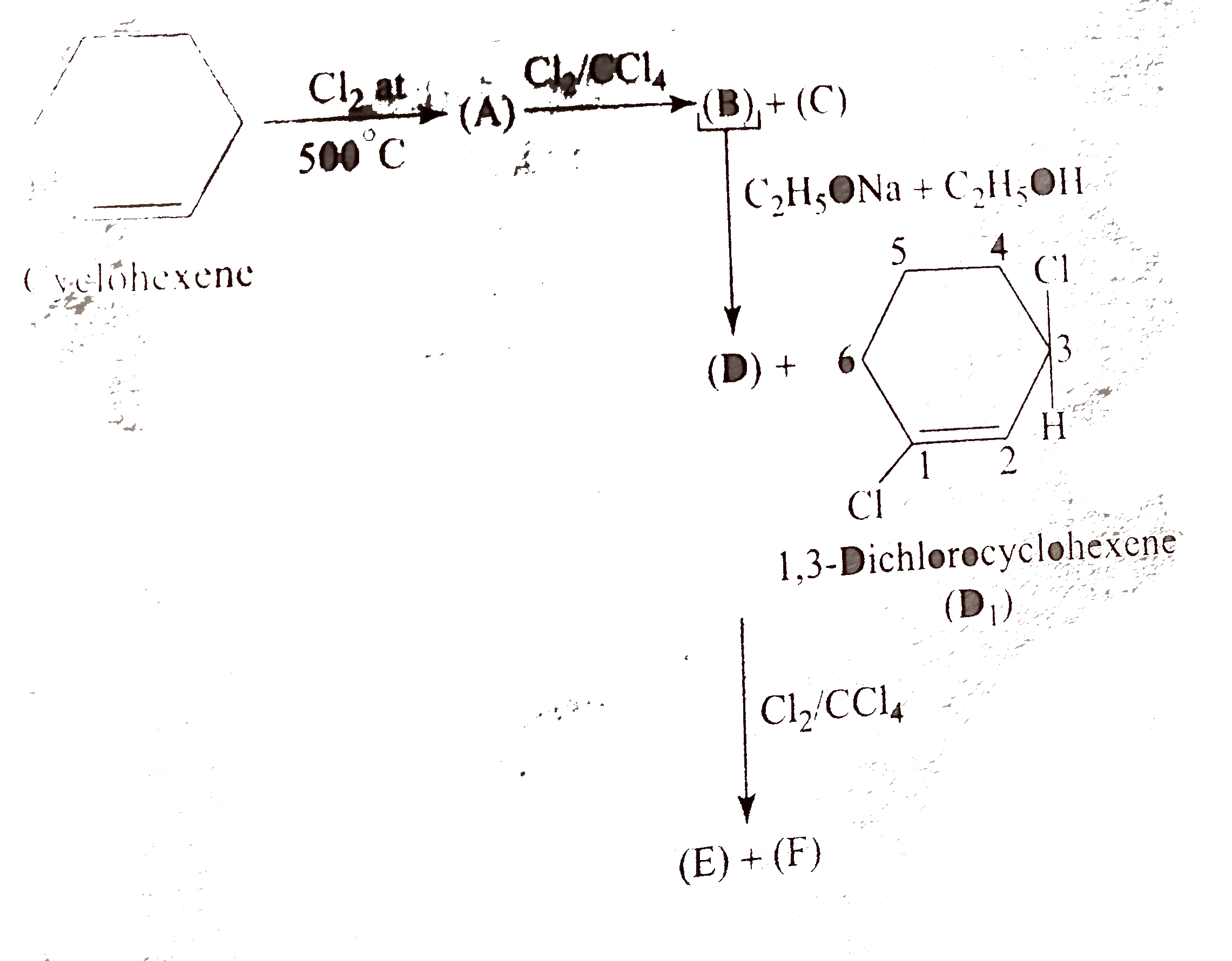
(E) and (F), respectively, are :A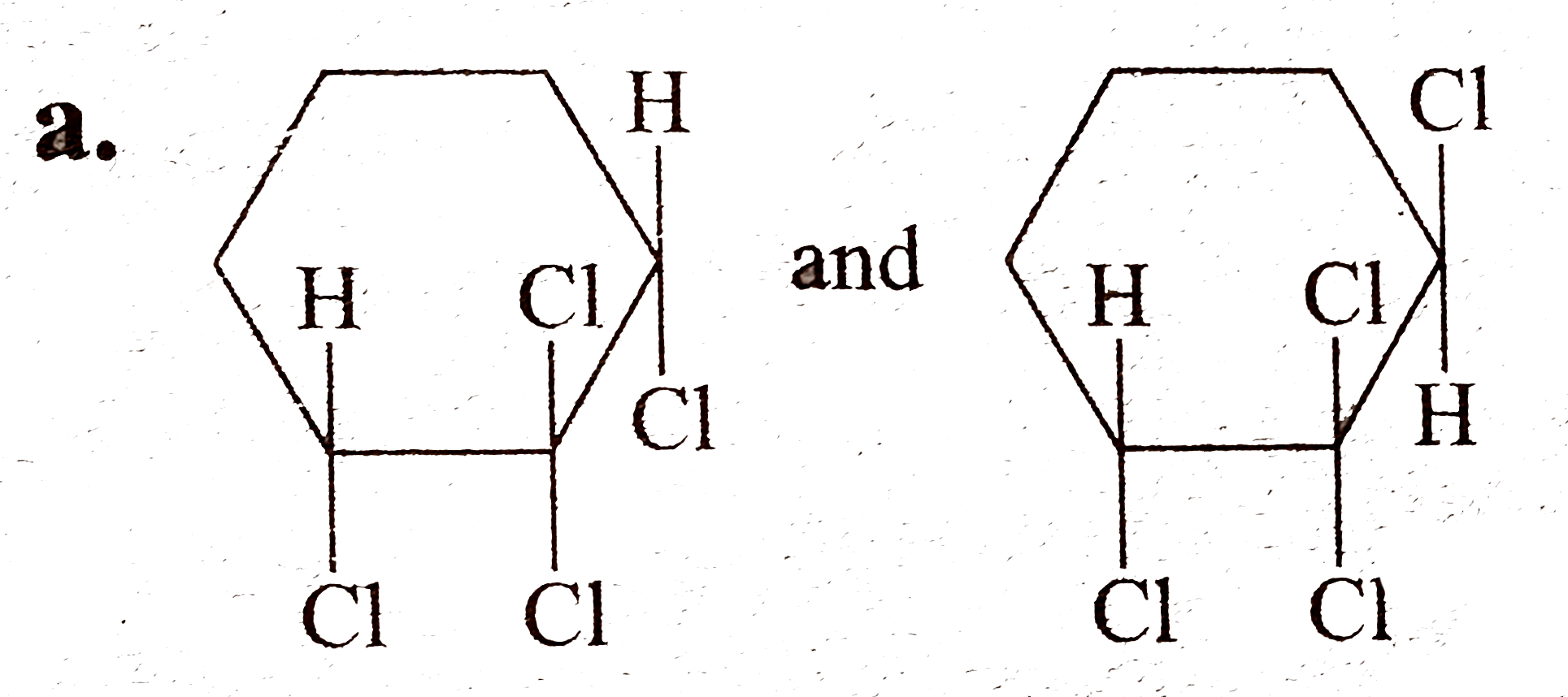 B
B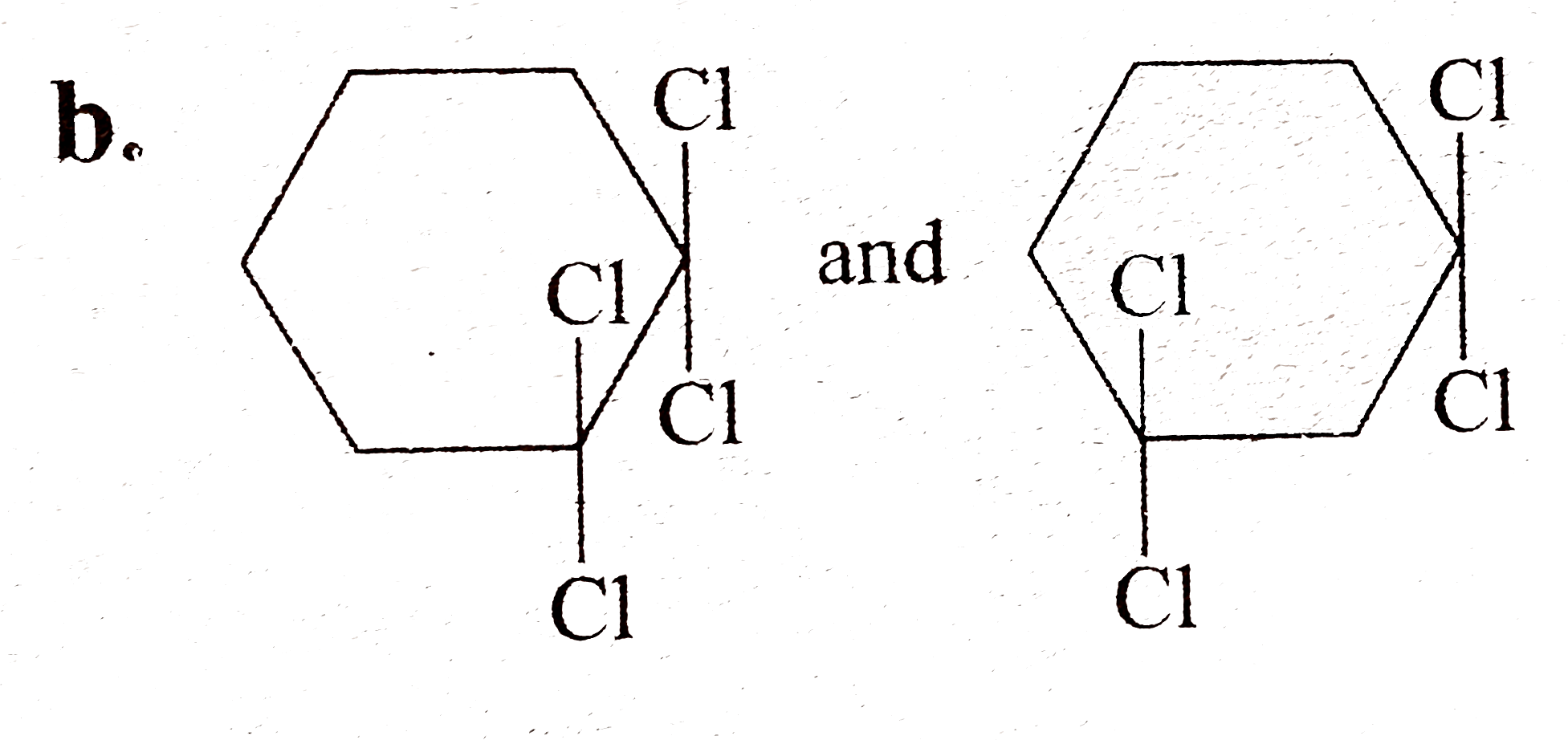 C
C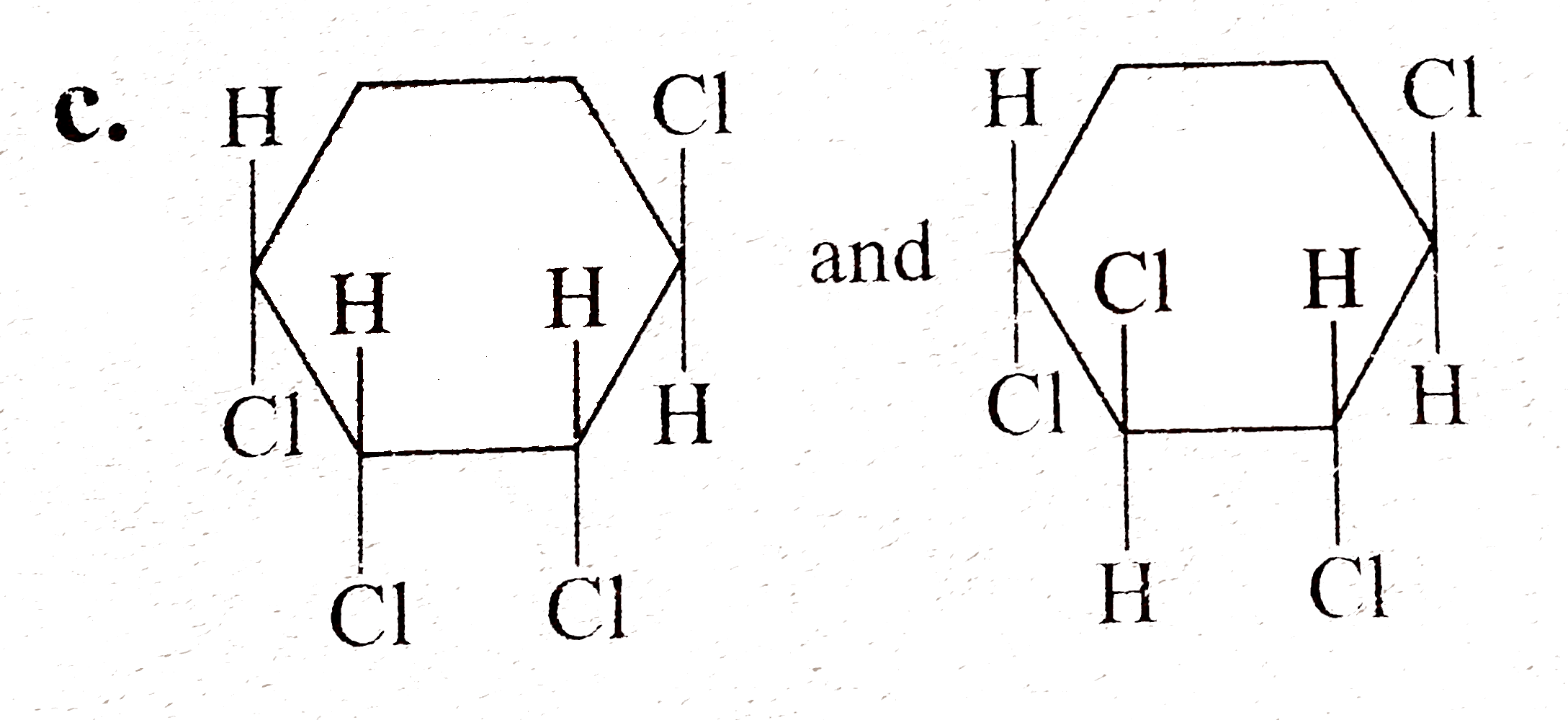 D
D
If F0 andFe are the focal lengths of the objective and eye-piece respectively for a Galilean telescope, its magnifying power is about
AF0+FeBF0×FeCF0/FeD12F0+FeIf A',B' are complementary events of two independent events A, B, then P(A∪B)=
A1−P(A)P(B')B1−P(A')P(B)C1−P(A')P(B')DP(A')+P(B')
If ¯¯¯E & ¯¯¯F are complementary events of events E&F respectively then P(EF)+P(¯¯¯EF)
View SolutionIf A and B are two complementary events, then what is the relation between P(A) and P(B).
View SolutionIf E and F are independent events with P(E)=p and P(F)=2p and P(exactly one of E,F) =56 then find the value of p
View SolutionIf E and F are two independent events then prove that E and F' are also independent events.
View SolutionUnits of van der Waal's constants a and bare respectively
View Solution
