If bisectors of ∠Aand∠B of a quadrilateral ABCD intersect each other at P, of ∠Band∠C at Q, of ∠Cand∠D at R and of ∠Dand∠A at S, then PQRS is a
A
rectangle
B
rhombus
C
parallelogram
D
quadrilateral whose opposite angles are supplementary
Video Solution
Text Solution
The correct Answer is:D
Given, ABCD is a quadrilateral and all angles bisectors form a quadrilateral PQRS.
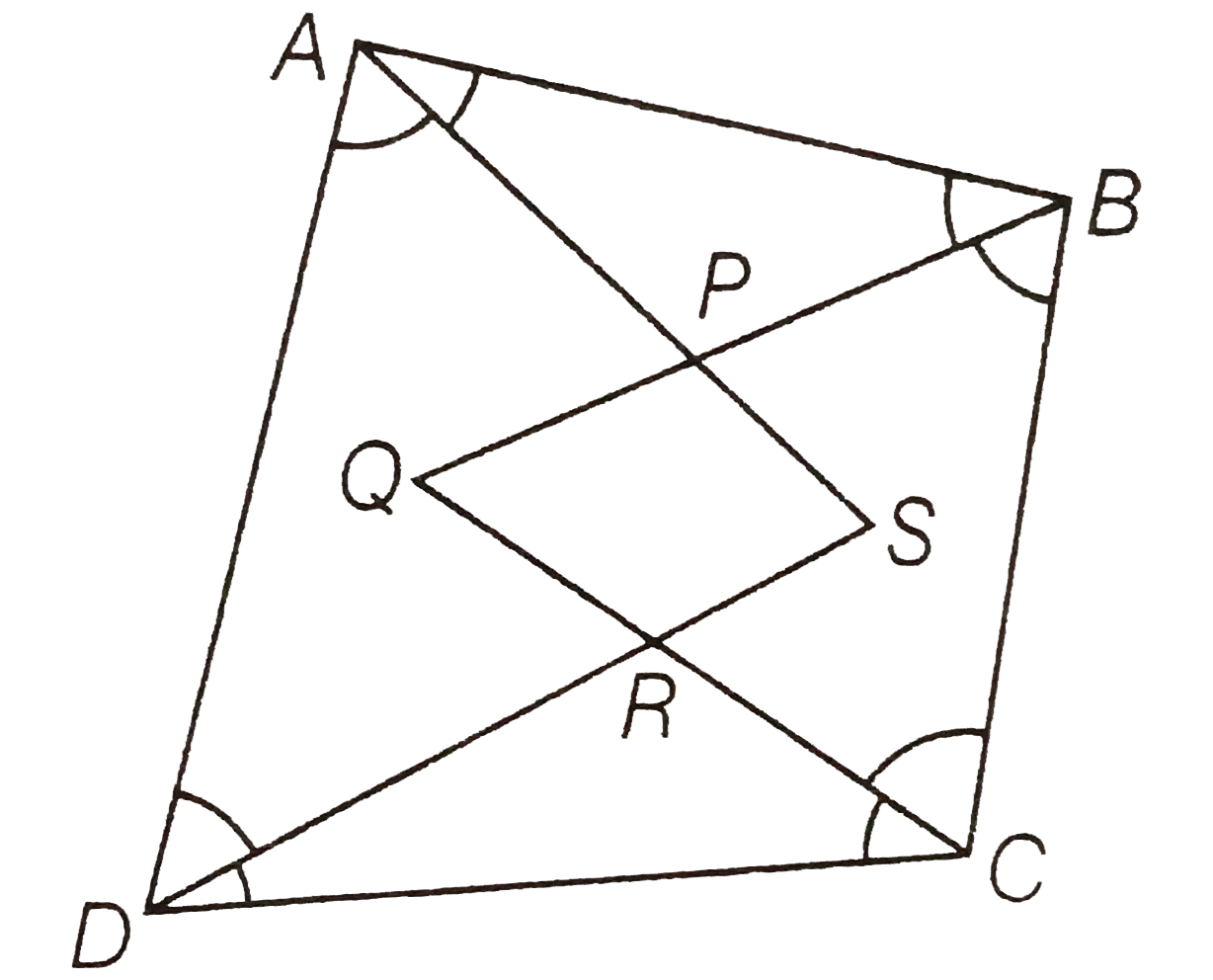 ltBrgt We know that, sum of all angles in a quadrilateral is 360∘.
ltBrgt We know that, sum of all angles in a quadrilateral is 360∘.
∴ ∠A+∠B+∠C+∠D=360∘
On dividing both sides by 2, we get
12(∠A+∠B+∠C+∠D)=360∘2 ltBrgt ⇒ ∠PAB+∠PBA+∠RCD+∠RDC=180∘ ...(i)
[since, AP and PB are the bisectors of ∠Aand∠B respectively also RC and RD are the bisectors of ∠Cand∠D respectively]
Now, in ΔAPB, ltBrgt ∠PAB+∠ABP+∠BPA=180∘
[by angle sum properly of a triangle]
⇒ ∠PAB+∠ABP=180∘−∠BPA ...(ii)
Similarly in ΔRDC, ltBrgt ∠RDC+∠DCR+∠CRD=180∘ ltBrgt [by angle sum property of a triangle]
⇒ ∠RDC+∠DCR=180∘−∠CRD ...(iii)
On substituting the value Eqs. (ii) and (iii) in Eq. (i), we get ltBrgt 180∘−∠BPA+180∘−∠DRC=180∘
⇒ ∠BPA+∠DRC=180∘ ltBrgt ⇒ ∠SPQ+∠SRQ=180∘
[∵∠BPA=∠SPQand∠DRC=∠SRQ vertically opposite angles]
Hence, PQRS is a quadrilateral whose opposite angles are suppolementary.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If bisectors of ∠Aand∠B of a quadrilateral ABCD intersect each other at P, of ∠Band∠C at Q, of ∠Cand∠D at R and of ∠Dand∠A at S then PQRS is a
ArectangleBparallelogramCrhombusDquardilateral whose opposite angles are supplementaryDiagonals of a quadrilateral ABCD bisect each other. If ∠A=35∘, determine ∠B.
A∠B=145∘B∠B=115∘C∠B=135∘D∠B=125∘
BO and CO are external bisector of ∠B and ∠C of △ABC intersecting at O. If internal bisector of ∠B and ∠C intersect at P, prove that ∠PBO=90∘ and ∠BOC+∠BPC=180∘
View SolutionAB and CD are respectively the smallest and largest sides of a quadrilateral ABCD. Show that ∠A>∠Cand∠B>∠C.

View SolutionIn a △ABC,if 2∠A=3∠B=6∠C calculate ∠A,∠B and ∠C
View SolutionBO and CO are external bisector of ∠B and ∠C of △ABC intersecting at O. If ∠A=60∘,∠ABC=70∘, Find ∠BOC
View SolutionBO and CO are external bisector of ∠B and ∠C of △ABC intersecting at O. If ∠A=60∘,∠ABC=70∘, Find ∠BOC
View SolutionIf ∠A and ∠B are supplementary angles. If 4∠A=5∠B, then find ∠A and ∠B.
View Solution
