If D, E, f are the mid-point of the sides of triangle ABC, prove that : ar(△DEF)=14ar(△ABC).Solution in Punjabi
Step by step video & image solution for If D, E, f are the mid-point of the sides of triangle ABC, prove that : ar(/_\DEF)=1/4 ar(/_\ABC). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Represent graphically a displacement of 40 km, 30o west of south.
View SolutionIf →a is a unit vcetor and (→x−→a)⋅(→x+→a)=80, then find |→x|.
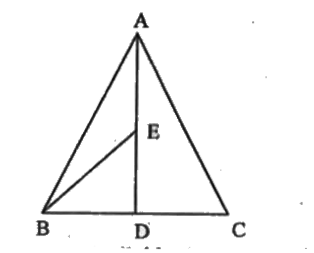
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar (BED)=14ar (ABC)
View SolutionD, E और F क्रमशः त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य-बिन्दु है। दर्शाइए कि :
(i) BDEF का समान्तर चतुर्भुज है।
(ii) ar(DEF)=14ar(ABC)
(iii) ar(BDEF)=12ar(ABC)
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar (BED) = 14 ar (ABC).
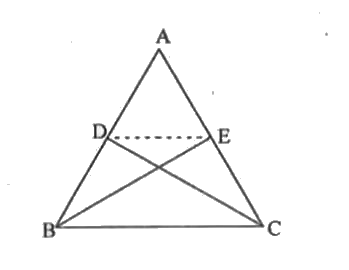
View SolutionD and E are points on sides AB and AC respectively of Δ ABC such that ar (DBC) = ar EBC). Prove that DE∣∣BC.
View SolutionIn a triangle ABC, E is the mid - point of median AD. Show that ar (BED) =1/4 ar (ABC)
View SolutionD,E and F are respectively the mid-points of the sides BC, CA and AB of △ABC show that
(i) BDEF is a parallelogram.
(ii) ar (DEF) = 14 ar (ABC)
(iii) ar(BDEF)=12 ar (ABC)
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE)=14 ar(ABC).
View SolutionD, E and F are the midpoints of triangles ABC BC, CA and AB respectively. ar (DEF) =1/4 ar (ABC)
View SolutionABC ত্রিভুজের AB, BCও CA বাহুর মধ্যবিন্দুগুলি যথাক্রমে D, E ও F। প্রমাণ করো, △DEF=14△ABC।
View SolutionIf D,E,F are mid-points of the sides of triangle ABC , prove (by vectors) that area of triangle DEF= 1/4 area of triangle ABC .
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar (triangleBED)=1/4 ar( triangleABC ).
View SolutionD is the mid-point of side BC of Delta ABC and E is the mid-point of BO. If O is the mid-point of AE, then ar( Delta BOE) = 1/k ar( Delta ABC). Then k equals
View SolutionE is any point on median AD of a △ABC . Show that ar (ABE) = ar (ACE).
View Solution
